题目内容
9.若复数z满足(1+i)z=3+i,则复数z的共轭复数在复平面内所对应的点的坐标是( )| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
分析 利用复数的运算法则、共轭复数的定义、几何意义即可得出.
解答 解:∵(1+i)z=3+i,∴z=$\frac{3+i}{1+i}$=$\frac{(3+i)(1-i)}{(1+i)(1-i)}$=$\frac{4-2i}{2}$=2-i,
∴则复数z的共轭复数$\overline{z}$=2+i在复平面内所对应的点的坐标是(2,1).
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义、几何意义,属于基础题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20.已知函数f(x)=ln(1-$\frac{a}{x+1}$)(a∈R),命题p:?a∈R,f(x)是奇函数,命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题是真命题的是( )
| A. | ¬p | B. | p∧q | C. | (¬p)∧q | D. | p∧(¬q) |
17.一个几何体的三视图如图所示,则该几何体的体积为( )
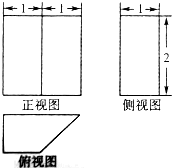

| A. | $\frac{2}{3}$ | B. | 1 | C. | 3 | D. | 6 |
18.若复数z1=1+i,z2=1-i,则复数$\frac{{z}_{2}}{{z}_{1}}$的模是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |