题目内容
19.在(2x+$\frac{1}{x^2}$)6的二项式中,常数项等于240(结果用数值表示).分析 写出二项展开式的通项,由x的指数为0求得r值,则答案可求.
解答 解:由(2x+$\frac{1}{x^2}$)6,得
${T}_{r+1}={C}_{6}^{r}(2x)^{6-r}•(\frac{1}{{x}^{2}})^{r}$=${2}^{6-r}•{C}_{6}^{r}•{x}^{6-3r}$.
由6-3r=0,得r=2.
∴常数项等于${2}^{4}×{C}_{6}^{2}=240$.
故答案为:240.
点评 本题考查了二项式系数的性质,关键是对二项展开式通项的记忆与运用,是基础题.

练习册系列答案
相关题目
9.若复数z满足(1+i)z=3+i,则复数z的共轭复数在复平面内所对应的点的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
18.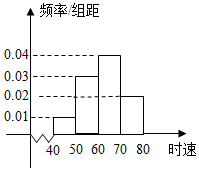 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )| A. | 60 | B. | 65 | C. | 60.5 | D. | 70 |
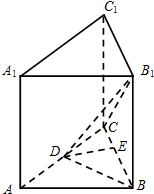 如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.
如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.