题目内容
20.已知函数f(x)=ln(1-$\frac{a}{x+1}$)(a∈R),命题p:?a∈R,f(x)是奇函数,命题q:?a∈R,f(x)在定义域内是增函数,那么下列命题是真命题的是( )| A. | ¬p | B. | p∧q | C. | (¬p)∧q | D. | p∧(¬q) |
分析 根据奇函数定义及复合函数的单调知命题p是真,命题q是假,问题得以解决.
解答 解:若f(x)是奇函数,则f(0)=0,
∴ln(1-a)=0,即1-a=1,解得a=0,
∴命题p:?a∈R,f(x)是奇函数是真命题,则¬p为假命题,
t=1-$\frac{a}{x+1}$,当a>0时,为增函数,当a<0时,为减函数,
∴当a>0时,f(x)为增函数,当a<0时,f(x)为减函数,
∴命题q:?a∈R,f(x)在定义域内是增函数是假命题,故¬q为真命题,
故选:D.
点评 本题借助考查复合命题的真假判断,考查了对数函数的奇偶性及复合函数的单调性,解题的关键是熟练掌握复合命题的真假规律.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
10.函数y=lg(-x2+2x+8)的增区间为( )
| A. | (-∞,1] | B. | [1,+∞) | C. | (-2,1] | D. | [1,4) |
8.直线x=0的斜率为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | 1 | D. | 不存在 |
12.设椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上一点P,点P在第一象限,且OP与x轴正方向所成角∠POX=$\frac{π}{3}$,求点P的坐标.
9.若复数z满足(1+i)z=3+i,则复数z的共轭复数在复平面内所对应的点的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
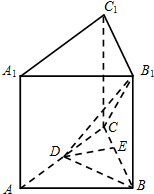 如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.
如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.