题目内容
1．直线a、b为异面直线，过直线a与直线b平行的平面有多少个，试说明理由．分析 先取直线a上任一点A并过A点作直线c∥b，由公理2的两个推论分别确定两个平面，再由线面平行的判定定理推出
解答 解：有且只有一个；
取直线a上任一点A，则点A和直线b确定一个平面记为β，在β内过A点作直线c∥b，
由a∩c=A，则直线a、c确定唯一的平面记为α，
∵c∥b，c?α，b?α，∴b∥α有且仅有一个．
假设过直线a与直线b平行的平面有两个或者两个以上，那么与两条相交直线确定一个平面矛盾；
所以过直线a与直线b平行的平面有且只有一．个
点评 本题考查了空间中异面直线的位置关系，利用公理2的两个推论和线面平行的判定定理判断出正确选项
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．设椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上一点P，点P在第一象限，且OP与x轴正方向所成角∠POX=$\frac{π}{3}$，求点P的坐标．
9．若复数z满足（1+i）z=3+i，则复数z的共轭复数在复平面内所对应的点的坐标是（ ）
| A． | （-2，-1） | B． | （2，-1） | C． | （-2，1） | D． | （2，1） |
6．已知全集U=R，A={x|2＜3x≤9}，B={y|$\frac{1}{2}$＜y≤2}，则有（ ）
| A． | A?B | B． | A∩B=B | C． | A∩（∁RB）≠∅ | D． | A∪（∁RB）=R |
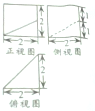
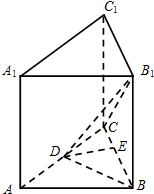如图，直三棱柱ABC-A1B1C1中，∠BAC=$\frac{π}{2}$，D为AC中点，E为BC上一点，且∠CDE=∠ABC．