题目内容
17.一个几何体的三视图如图所示,则该几何体的体积为( )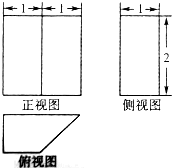
| A. | $\frac{2}{3}$ | B. | 1 | C. | 3 | D. | 6 |
分析 由已知的三视图可得:该几何体是一个以俯视图为底面的四棱柱,计算出柱体的底面面积和高,代入棱柱体积公式,可得答案.
解答 解:由已知的三视图可得:该几何体是一个以俯视图为底面的四棱柱,
棱柱的底面是一个上底为1,下底为2,高为1的梯形,
故底面面积S=$\frac{1}{2}$×(1+2)×2=3,
棱柱的高h=2,
故棱柱的体积V=Sh=6,
故选:D.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
7.某中学为了解学校办公楼每天的用电量x(度)与当天最高气温x(℃)之间的关系,随机统计了近期某4天的有关数据如下表示:
据回归分析,上述4线样本数据具有线性相关关系,计算得回归直线的斜率b=-3.2,由回归方程可以预报最高气温为6℃时当天的用电量约为( )
| 最高气温x(℃) | 10 | 4 | -2 | -8 |
| 用电量y(度) | 20 | 44 | 56 | 80 |
| A. | 32度 | B. | 34度 | C. | 36度 | D. | 38度 |
8.直线x=0的斜率为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | 1 | D. | 不存在 |
12.设椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上一点P,点P在第一象限,且OP与x轴正方向所成角∠POX=$\frac{π}{3}$,求点P的坐标.
9.若复数z满足(1+i)z=3+i,则复数z的共轭复数在复平面内所对应的点的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (-2,1) | D. | (2,1) |
6.已知全集U=R,A={x|2<3x≤9},B={y|$\frac{1}{2}$<y≤2},则有( )
| A. | A?B | B. | A∩B=B | C. | A∩(∁RB)≠∅ | D. | A∪(∁RB)=R |