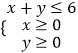题目内容
【题目】某综艺频道举行某个水上娱乐游戏,如图,固定在水面上点![]() 处的某种设备产生水波圈,水波圈生产
处的某种设备产生水波圈,水波圈生产![]() 秒时的半径
秒时的半径![]() (单位:
(单位: ![]() )满足
)满足![]() ;
; ![]() 是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端
是铺设在水面上的浮桥,浮桥的宽度忽略不计,浮桥两端![]() 固定在水岸边.游戏规定:当点
固定在水岸边.游戏规定:当点![]() 处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的
处刚产生水波圈时,游戏参与者(视为一个点)与此同时从浮桥的![]() 端跑向
端跑向![]() 端;若该参与者通过浮桥
端;若该参与者通过浮桥![]() 的过程中,从点
的过程中,从点![]() 处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知
处发出的水波圈始终没能到达此人跑动时的位置,则认定该参与者在这个游戏中过关;否则认定在这个游戏中不过关,已知![]() ,
, ![]() ,浮桥
,浮桥![]() 的某个桥墩处点
的某个桥墩处点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,且
,且![]() ,若某游戏参与者能以
,若某游戏参与者能以![]() 的速度从浮桥
的速度从浮桥![]() 端匀速跑到
端匀速跑到![]() 端.
端.
(1)求该游戏参与者从浮桥![]() 端跑到
端跑到![]() 端所需的时间?
端所需的时间?
(2)问该游戏参与者能否在这个游戏中过关?请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)设![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() (舍).求得直线
(舍).求得直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立可得
联立可得![]() ,求得AB,进而可得所需时间;
,求得AB,进而可得所需时间;
(2)求得![]() 时,点
时,点![]() 坐标为
坐标为![]() ,其中
,其中![]() .
. ![]() ,
, ![]() .构造函数
.构造函数![]()
![]() ,求导计算可得
,求导计算可得![]() 时,
时, ![]() 恒成立,所以该参与者在这个游戏中过关.
恒成立,所以该参与者在这个游戏中过关.
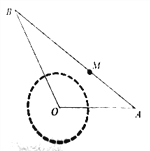
试题解析:(1)建立如图所示的直角坐标系,则![]() ,
,
直线![]() 的方程为
的方程为![]() .
.
设![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时, ![]() ,符合;
,符合;
当![]() 时,
时, ![]() ,不符合.
,不符合.
所以![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
由![]() 解得
解得![]() 即
即![]() .
.
所以![]() .
.
所以,该游戏参与者从浮桥![]() 端跑到
端跑到![]() 端所需的时间为
端所需的时间为![]() .
.
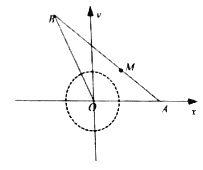
(2)在![]() 中,
中, ![]() ,
, ![]() .
.
设![]() 时,该参与者位于点
时,该参与者位于点![]() ,则
,则![]() ,
, ![]() .
.
则![]() 时,点
时,点![]() 坐标为
坐标为![]() ,其中
,其中![]() .
.
![]() ,
, ![]() .
.
令![]()
![]() ,
,
则![]()
![]()
![]() 时
时![]() ,
, ![]() 在
在![]() 上为增函数,
上为增函数,
![]() 时
时![]() ,
, ![]() 在
在![]() 上为减函数,
上为减函数,
故当![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
由于![]() ,所以
,所以![]() 时,
时, ![]() 恒成立.
恒成立.
即该游戏参与者通过浮桥![]() 的过程中,从点
的过程中,从点![]() 处发出的水波圈始终没能到达此人跑动时的位置,所以该参与者在这个游戏中过关.
处发出的水波圈始终没能到达此人跑动时的位置,所以该参与者在这个游戏中过关.
点晴:本题考查的是函数模型的应用。解决函数模型应用的解答题,要注意以下几点:①读懂实际背景,将实际问题转化为函数模型.②对涉及的相关公式,记忆要准确.③在求解的过程中计算要正确.另外需要熟练掌握求解方程、不等式、函数最值的方法,才能快速正确地求解.