题目内容
【题目】解答
（1）将一颗骰子（一种各个面上分别标有1，2，3，4，5，6个点的正方体玩具）先后抛掷2次，以分别得到的点数（m，n）作为点P的坐标（m，n），求：点P落在区域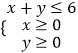 
内的概率；
（2）在区间[1，6]上任取两个实数（m，n），求：使方程x2+mx+n2=0有实数根的概率．
【答案】
（1）解：抛掷2次骰子共包括36个基本事件，每个基本事件都是等可能的．…（1分）
记“点P落在区域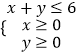 
内”为事件A，
事件A包括下列15个基本事件：15；
所以 
．
答：点P落在内的概率为 
（2）解：记“方程x2+mx+n2=0有实数根”为事件B，…（8分）
在区间[1，6]上任取两个实数（m，n），可看作是在区域D： 
内随机取一点，
每个点被取到的机会是均等的；
而事件B发生，则视作点（m，n），恰好落在区域d：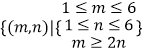 
所以 
答：使方程x2+mx+n2=0有实数根的概率为 
【解析】（1）由题意知是一个古典概型，由分步计数原理知试验发生的总事件数是6×6，记“点P落在区域 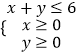内”为事件A，事件A包括下列15个基本事件：15，即可求点P落在区域 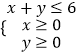内的概率；（2）在区间[1，6]上任取两个实数（m，n），确定平面区域，求出相应的面积，即可求：使方程x2+mx+n2=0有实数根的概率．
【考点精析】认真审题，首先需要了解几何概型(几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等)．
练习册系列答案
相关题目
