题目内容
【题目】设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),则a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
【答案】B
【解析】解:Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1), 可得Sn+12﹣2Sn+1Sn﹣3Sn2+Sn+1﹣3Sn=0,
即有(Sn+1﹣3Sn)(Sn+1+Sn)+(Sn+1﹣3Sn)=0,
即为(Sn+1﹣3Sn)(Sn+1+Sn+1)=0,
即有Sn+1=3Sn ,
数列{Sn}为等比数列,首项为2,公比为3,
可得Sn=2×3n﹣1 ,
则a100=S100﹣S99=2×399﹣2×398
=4×398 .
故选:B.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系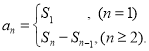 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目