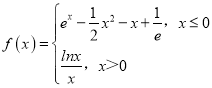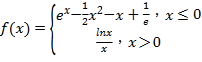��Ŀ����
����Ŀ��Ϊӭ��2022�걱���������˻ᣬ�ռ�����֪ʶ��ijУ��չ������ѩ������������֪ʶ�����.�ִӲμӶ���֪ʶ�������ѧ���������ȡ��100��ѧ���������ǵı����ɼ�������Ϊ100�֣�����Ϊ6�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
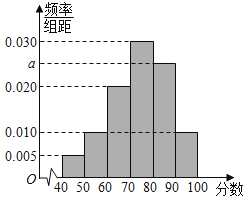
��1����![]() ��ֵ��
��ֵ��
��2����![]() ��ʾ�¼����ӲμӶ���֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80����������
��ʾ�¼����ӲμӶ���֪ʶ�������ѧ���������ȡһ��ѧ������ѧ���ı����ɼ�������80����������![]() �ĸ��ʣ�
�ĸ��ʣ�
��3���ڳ�ȡ��100��ѧ���У��涨�������ɼ�������80��Ϊ�����������������ɼ�����80��Ϊ����������.�뽫�����![]() �������������������ж��Ƿ���99.9%�İ�����Ϊ�������ɼ��Ƿ��������Ա��й���?
�������������������ж��Ƿ���99.9%�İ�����Ϊ�������ɼ��Ƿ��������Ա��й���?
���� | ������ | �ϼ� | |
���� | 40 | ||
�� | 50 | ||
�ϼ� | 100 |
�ο���ʽ�����ݣ�![]() ��
��![]() .
.
���𰸡���1��![]() ����2��
����2��![]() ����3����������������û��
����3����������������û��
��������
��1���������ϸ���Ƶ�ʺ�Ϊ1���ɵý⣻
��2����������������ɼ�������80�ֵ�Ƶ�ʣ��������������弴�ɵý⣻
��3����������������������빫ʽ���![]() ����
����![]() �ȽϺɵý�.
�ȽϺɵý�.
��1��������![]() ��
��
��![]() ��
��
��2����Ƶ�ʷֲ�ֱ��ͼ�ɵ������б����ɼ�������80�ֵ�Ƶ��Ϊ��![]() ��
��
��ɹ���![]() �ĸ���Ϊ0.35��
�ĸ���Ϊ0.35��
��3����Ƶ�ʷֲ�ֱ��ͼ��֪��ȡ��100��ѧ���У����������Ϊ![]() ��
��
���������£�
���� | ������ | �ϼ� | |
���� | 10 | 40 | 50 |
�� | 25 | 25 | 50 |
�ϼ� | 35 | 65 | 100 |
��![]() ��
��
�����![]() �İ�����Ϊ�����ɼ��Ƿ��������Ա��й�.
�İ�����Ϊ�����ɼ��Ƿ��������Ա��й�.

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�����Ŀ��ͨ�����ѯ��![]() ����ͬ�Ա�Ĵ�ѧ���Ƿ�ij���˶����õ����µ�
����ͬ�Ա�Ĵ�ѧ���Ƿ�ij���˶����õ����µ�![]() ��������
��������
�� | ٠| |
���� | 40 | 20 |
������ | 20 | 30 |
��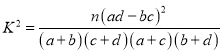 ���
���![]() ��
��
���ո��������²���ȷ���У� ��
������
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.�ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ�����ø����˶����Ա��й���
��ǰ���£���Ϊ�����ø����˶����Ա��й���
B.�ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ�����ø����˶����Ա�����
��ǰ���£���Ϊ�����ø����˶����Ա�����
C.��![]() ���ϵİ�����Ϊ�����ø����˶����Ա��й���
���ϵİ�����Ϊ�����ø����˶����Ա��й���
D.��![]() ���ϵİ�����Ϊ�����ø����˶����Ա�����
���ϵİ�����Ϊ�����ø����˶����Ա�����