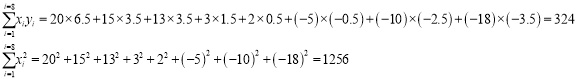题目内容
【题目】已知函数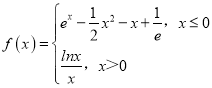 ,若方程f(x)﹣m=0恰有两个实根,则实数m的取值范围是_____.
,若方程f(x)﹣m=0恰有两个实根,则实数m的取值范围是_____.
【答案】![]()
【解析】
通过求导,得出分段函数各段上的单调性,从而画出图像.若要方程f(x)﹣m=0恰有两个实根,只需y=m与y=f(x)恰有两个交点即可,从而得出![]() 的取值范围.
的取值范围.
(1)x≤0时,f′(x)=ex﹣x﹣1,易知f′(0)=0,而f″(x)=ex﹣1<0,
所以f′(x)在(﹣∞,0]上递减,故f′(x)≥f′(0)=0,故f(x)在(﹣∞,0]上递增,
且f(x)≤f(0)![]() ,当x→﹣∞时,f(x)→﹣∞.
,当x→﹣∞时,f(x)→﹣∞.
(2)x>0时,![]() ,令f′(x)>0,得0<x<e;f′(x)<0得x>e;
,令f′(x)>0,得0<x<e;f′(x)<0得x>e;
故f(x)在(0,e)上递增,在(e,+∞)递减,
故x>0时,![]() ;x→0时,f(x)→﹣∞;x→+∞时,f(x)→0.
;x→0时,f(x)→﹣∞;x→+∞时,f(x)→0.
由题意,若方程f(x)﹣m=0恰有两个实根,只需y=m与y=f(x)恰有两个交点,同一坐标系画出它们的图象如下:
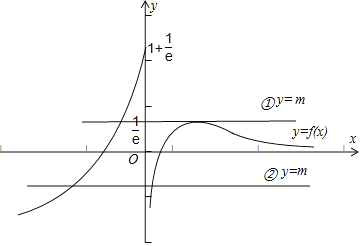
如图所示,当直线y=m在图示①,②位置时,与y=f(x)有两个交点,所以m的范围是:![]() .
.
故答案为:![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】某理财公司有两种理财产品![]() 和
和![]() ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品![]() (其中
(其中![]() )
)
投资结果 | 获利30% | 不赔不赚 | 亏损20% |
概率 |
| 0.1 |
|
(1)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求![]() 的取值范围;
的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?
【题目】偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)若![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该次考试该数平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据: