Question

【题目】已知圆，点，是圆上任意一点，线段的垂直平分线交于点，当点在圆上运动时，点的轨迹为曲线．

1求曲线的方程；

2若直线 与曲线相交于两点，为坐标原点，求面积的最大值．

Answer 1

【答案】（Ⅰ）;（Ⅱ）．

【解析】

试题（1）由垂直平分线的几何意义可知，，满足椭圆的定义。（2）直线与椭圆组方程组，由韦达定理、弦长公式和点到直线的距离公式，可求得 ．由，得及均值不等式可求得面积的最大值．

试题解析：（Ⅰ）∵点在线段的垂直平分线上，∴．

又，∴．

∴曲线是以坐标原点为中心，和为焦点，长轴长为的椭圆．

设曲线的方程为．

∵，∴．

∴曲线的方程为．

（Ⅱ）设．

联立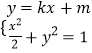消去，得．

此时有．

由一元二次方程根与系数的关系，得

，．

∴ ．

∵原点到直线的距离，

∴ ．

由，得．又，∴据基本不等式，得

．

当且仅当时，不等式取等号．

∴面积的最大值为．