题目内容
(本小题满分12分)
如图,在正三棱柱ABC—A1B1C1中,BB1=2,BC=2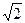 ,D为B1C1的中点。
,D为B1C1的中点。
(Ⅰ)证明:B1C⊥面A1BD;
(Ⅱ)求二面角B—AC—B1的大小。
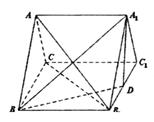
如图,在正三棱柱ABC—A1B1C1中,BB1=2,BC=2
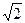 ,D为B1C1的中点。
,D为B1C1的中点。(Ⅰ)证明:B1C⊥面A1BD;
(Ⅱ)求二面角B—AC—B1的大小。

方法一:
(Ⅰ)证明:在Rt△BB1D和Rt△B1C1C中,
由
 得
得△BB1D∽△B1C1C,∠B1DB=∠B1CC1。
又 ∠CB1D+∠B1CC1=90°
故 ∠CB1D+∠B1DB=90°
故 B1C⊥BD.·····················3分
又 正三棱柱ABC—A1B1C1,D为B1C1的中点。
由 A1D⊥平面B1C,
得 A1D⊥B1C
又A1D∩B1D=D,
所以 B1C⊥面A1BD。···················································6分
(Ⅱ)解:设E为AC的中点,连接BE.B1E。
在正三棱柱ABC—A1B1C1中,B1C=B1A,∴B1E⊥AC,BE⊥AC,
即 ∠BEB1为二面角B—AC—B1的平面角·································9分
又

故

所以 二面角的大小为
 ······································12分
······································12分方法二:
(Ⅰ)证明:设BC的中点为O,如图建立空间直角坐标系O—xyz
依题意有
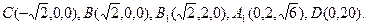
则

由
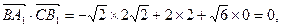
故
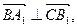
又

所以

故
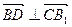
又 BD∩BA1=B
所以 B1C⊥面A1BD,
(Ⅱ)依题意有

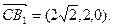
设
 ⊥平面ACB1,
⊥平面ACB1, ⊥平面ABC。
⊥平面ABC。求得

故
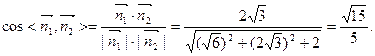
所以 二面角的大小为

略

练习册系列答案
相关题目
 ,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB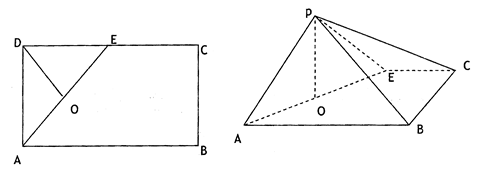 (1)求证:PO⊥面ABCE;
(1)求证:PO⊥面ABCE;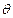 的正弦值.
的正弦值. 锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB
锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB ,PC的中点.
,PC的中点. (3)在(2)的条件下,若AB=2,AC=
(3)在(2)的条件下,若AB=2,AC= ,求三棱锥P-ABC的体积
,求三棱锥P-ABC的体积

 ,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点.
,底面ABCD为直角梯形,BC∥AD, AB⊥AD, AD=2AB=2BC="2, " O为AD中点. D所成角的正弦值;
D所成角的正弦值; 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。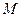 是棱
是棱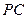 的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: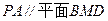 ;
;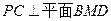 ;
;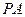 与直线
与直线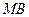 所成角的余弦值.
所成角的余弦值.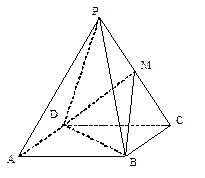

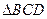 中,
中,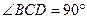 ,
,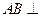 平面
平面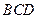 ,
,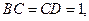
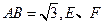 分别为
分别为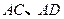 的中点.
的中点.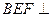 平面
平面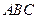 ;
;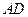 与平面
与平面 所成角的正弦值.
所成角的正弦值.