题目内容
(本题满分12分)
如图,在三棱 锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB
锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB ,PC的中点.
,PC的中点.
(1)在BC边上是否存在一点F,使得PB∥平面DEF
(2)若∠PAC=∠PBC=90º,证明:AB⊥PC
 (3)在(2)的条件下,若AB=2,AC=
(3)在(2)的条件下,若AB=2,AC= ,求三棱锥P-ABC的体积
,求三棱锥P-ABC的体积

如图,在三棱
 锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB
锥P-ABC中,⊿PAB是等边三角形,D,E分别为AB ,PC的中点.
,PC的中点.(1)在BC边上是否存在一点F,使得PB∥平面DEF
(2)若∠PAC=∠PBC=90º,证明:AB⊥PC
 (3)在(2)的条件下,若AB=2,AC=
(3)在(2)的条件下,若AB=2,AC= ,求三棱锥P-ABC的体积
,求三棱锥P-ABC的体积
解(1)取BC的中点为F,则有
PB∥平面DEF.
∵PB∥EF
PB不在平面DEF内
PB∥平面DEF………… …………4分
…………4分
(2)因为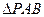 是等边三角形,
是等边三角形,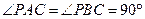 ,
,
所以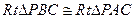 ,可得
,可得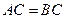 。
。
如图,取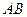 中点
中点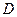 ,连结
,连结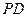 ,
,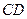 ,∴
,∴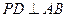 ,
,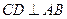 , ∴
, ∴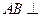 平面
平面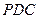 ,∴
,∴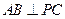 …………………8分
…………………8分
(3)∵PD=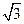 CD="2 " PC="3" ∴
CD="2 " PC="3" ∴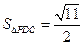
即三棱锥体积为: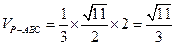 ………………………12分
………………………12分
PB∥平面DEF.
∵PB∥EF
PB不在平面DEF内
PB∥平面DEF…………
 …………4分
…………4分(2)因为
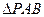 是等边三角形,
是等边三角形,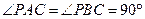 ,
,所以
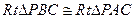 ,可得
,可得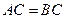 。
。
|
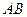 中点
中点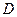 ,连结
,连结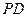 ,
,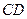 ,∴
,∴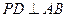 ,
,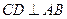 , ∴
, ∴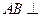 平面
平面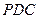 ,∴
,∴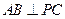 …………………8分
…………………8分
(3)∵PD=
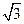 CD="2 " PC="3" ∴
CD="2 " PC="3" ∴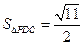
即三棱锥体积为:
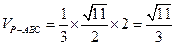 ………………………12分
………………………12分略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
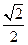 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 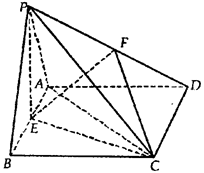
 为正三角形,
为正三角形,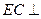 平面
平面 ,
,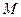 是
是 的中点,
的中点,
 平面
平面 。
。 ,D为B1C1的中点。
,D为B1C1的中点。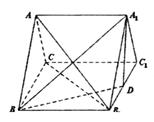
 中,
中, ,线段
,线段 的中点是
的中点是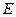 ,现将
,现将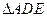 沿
沿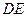 折起到
折起到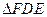 的位置,使平面
的位置,使平面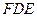 和平面
和平面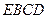 垂直,线段
垂直,线段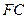 的中点是
的中点是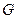 .
.
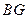 ∥平面
∥平面 和平面
和平面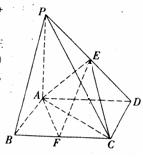
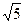 ,PD
,PD =4
=4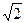 ,E是PD的中点
,E是PD的中点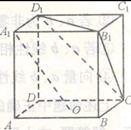
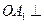 平面AB1C1
平面AB1C1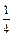 ,且
,且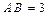 ,
,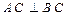 ,则球面的面积为 .
,则球面的面积为 .