题目内容
(本小题满分13分)
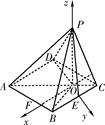
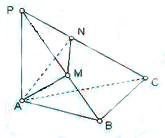
如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.
如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.

解:解法一:(Ⅰ)在菱形ABCD中,连接DB,则△BCD是等边三角形.
∵点E是BC边的中点
∴DE⊥BC.
∵PO⊥平面ABCD,
∴OD是斜线PD在底面ABCD内的射影.
∴PD⊥BC. (4分)

(Ⅱ)由(Ⅰ)知DE⊥BC,
菱形ABCD中,AD∥BC,
∴DE⊥AD.
又∵PO⊥平面ABCD,DE是PD在平面ABCD的射影,
∴PD⊥AD.
∴∠PDO为二面角P-AD-C的平面角.
在菱形ABCD中,AD⊥DE,由(1)知,△BCD为等边三角形,
∵点E是BC边的中点,AC与BD互相平分,
∴点O是△BCD重心.
∵AB=6,
又∵在等边△BDC中,
DO=DE=·BC=×6=6.
∴OC=OD=6.
∵PC=6,∴PO=6.
∴在Rt△POD中,tan∠PDO===1.
∴∠PDO=.
∴二面角P-AD-C的大小为. (9分)
(Ⅲ)取AD中点H,连接HB,HP.
则HB∥DE.
∴HB与PB所成角即是DE与PB所成角.
连接OH,OB.
∵PO⊥平面ABCD,OH,OB?平面ABCD,
∴PO⊥OH,PO⊥OB.
在Rt△DOH中,HD=3,OD=6,
∴OH=3.
在Rt△PHO中,PH==.
在Rt△POB中,OB=OC=6,PB==6.
由(Ⅱ)可知DE=HB=9.
设HB与PB所成角为α,
则cosα==.
∴异面直线PB、DE所成角的余弦值为. (13分)
解法二:(Ⅰ)同解法一; (4分)
(Ⅱ)过点O作AD平行线交AB于F,以点O为坐标原点,建立如图的坐标系.
∴A(6,-6,0),B(3,3,0),C(-3,3,0),
D(0,-6,0),P(0,0,6).
∴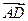 =(-6,0,0),
=(-6,0,0),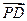 =(0,-6,-6).
=(0,-6,-6).
设平面PAD的一个法向量为s=(a,m,n).
则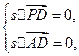
即
∴
不妨取s=(0,-1,1).
∵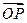 =(0,0,6)是平面ADC的一个法向量,
=(0,0,6)是平面ADC的一个法向量,
∴cos〈s,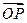 〉==.
〉==.
∴二面角P-AD-C的大小为. (9分)
(Ⅲ)由已知,可得点E(0,3,0).
∴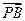 =(3,3,-6),
=(3,3,-6),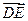 =(0,9,0).
=(0,9,0).
∴cos〈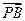 ,
,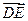 〉==.
〉==.
即异面直线PB、DE所成角的余弦值为.
∵点E是BC边的中点
∴DE⊥BC.
∵PO⊥平面ABCD,
∴OD是斜线PD在底面ABCD内的射影.
∴PD⊥BC. (4分)

(Ⅱ)由(Ⅰ)知DE⊥BC,
菱形ABCD中,AD∥BC,
∴DE⊥AD.
又∵PO⊥平面ABCD,DE是PD在平面ABCD的射影,
∴PD⊥AD.
∴∠PDO为二面角P-AD-C的平面角.
在菱形ABCD中,AD⊥DE,由(1)知,△BCD为等边三角形,
∵点E是BC边的中点,AC与BD互相平分,
∴点O是△BCD重心.
∵AB=6,
又∵在等边△BDC中,
DO=DE=·BC=×6=6.
∴OC=OD=6.
∵PC=6,∴PO=6.
∴在Rt△POD中,tan∠PDO===1.
∴∠PDO=.
∴二面角P-AD-C的大小为. (9分)
(Ⅲ)取AD中点H,连接HB,HP.
则HB∥DE.
∴HB与PB所成角即是DE与PB所成角.
连接OH,OB.
∵PO⊥平面ABCD,OH,OB?平面ABCD,
∴PO⊥OH,PO⊥OB.
在Rt△DOH中,HD=3,OD=6,
∴OH=3.
在Rt△PHO中,PH==.
在Rt△POB中,OB=OC=6,PB==6.
由(Ⅱ)可知DE=HB=9.
设HB与PB所成角为α,
则cosα==.
∴异面直线PB、DE所成角的余弦值为. (13分)
解法二:(Ⅰ)同解法一; (4分)
(Ⅱ)过点O作AD平行线交AB于F,以点O为坐标原点,建立如图的坐标系.
∴A(6,-6,0),B(3,3,0),C(-3,3,0),
D(0,-6,0),P(0,0,6).
∴
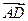 =(-6,0,0),
=(-6,0,0),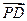 =(0,-6,-6).
=(0,-6,-6).
设平面PAD的一个法向量为s=(a,m,n).
则
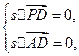
即
∴
不妨取s=(0,-1,1).
∵
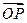 =(0,0,6)是平面ADC的一个法向量,
=(0,0,6)是平面ADC的一个法向量,∴cos〈s,
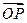 〉==.
〉==.∴二面角P-AD-C的大小为. (9分)
(Ⅲ)由已知,可得点E(0,3,0).
∴
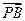 =(3,3,-6),
=(3,3,-6),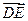 =(0,9,0).
=(0,9,0).∴cos〈
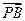 ,
,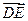 〉==.
〉==.即异面直线PB、DE所成角的余弦值为.
略

练习册系列答案
相关题目
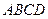 中,
中,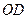 垂直平分
垂直平分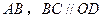 ,且
,且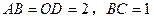 ,现将四边形
,现将四边形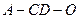 的正弦值;
的正弦值;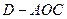 的体积。
的体积。
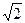 ,D为B1C1的中点。
,D为B1C1的中点。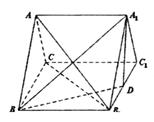
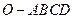 中,底面
中,底面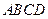 四边长为1的菱形,
四边长为1的菱形,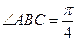 ,
,  ,
,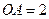 ,
,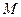 为
为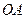 的中点,
的中点,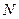 为
为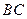 的中点
的中点 ;
;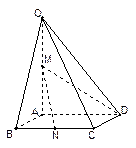
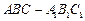 中,已知
中,已知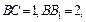
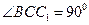 ,
,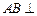 侧面
侧面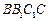
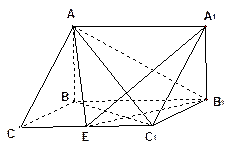
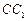 (不包含端点
(不包含端点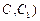 上确定一点
上确定一点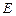 的位置,使得
的位置,使得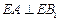 (要求说明理由).
(要求说明理由).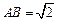 ,求二面角
,求二面角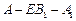 的大小.
的大小.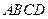 的顶点
的顶点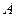 、
、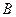 、
、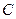 分别在两两垂直的三条射线
分别在两两垂直的三条射线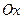 、
、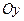 、
、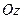 上,给出下列四个命题:
上,给出下列四个命题: 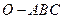 是正三棱锥;
是正三棱锥;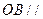 平面
平面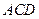 ;
;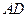 与
与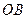 所成的角为
所成的角为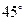 ;
; 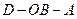 为
为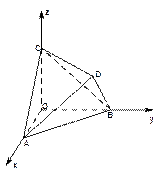
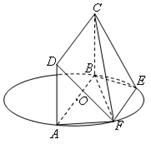
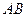 为圆
为圆 的直径,点
的直径,点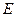 、
、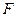 在圆
在圆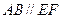 ,矩形
,矩形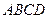 所在平面和圆
所在平面和圆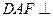 平面
平面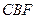 ;
;
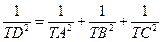 ;
;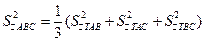 (注:
(注: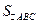 表示△ABC的面积)
表示△ABC的面积)