题目内容
4.已知函数f(x)=3sin(2x+$\frac{π}{4}$)(x∈R).(1)求函数f(x)的最小正周期和初相;
(2)若f($\frac{α}{2}$)=$\frac{9}{5}$,α∈($\frac{π}{4}$,$\frac{3π}{4}$),求cosα的值.
分析 (1)正弦函数y=Asin(ωx+θ)的周期T=$\frac{2π}{|ω|}$,初相是φ;
(2)把f($\frac{α}{2}$)=$\frac{9}{5}$代入函数解析式求得sin(α+$\frac{π}{4}$)=$\frac{3}{5}$,然后利用公式sin2α+cos2α=1和α的取值范围得到cos(α+$\frac{π}{4}$)=-$\frac{4}{5}$,所以cos=cos[(α+$\frac{π}{4}$)-$\frac{π}{4}$],利用两角和与差的余弦将其展开,并代入相关数值进行求值即可.
解答 解:(1)函数f(x)的最小正周期T=$\frac{2π}{2}$=π,初相φ=$\frac{π}{4}$;
(2)由f($\frac{α}{2}$)=$\frac{9}{5}$,得
3sin(α+$\frac{π}{4}$)=$\frac{9}{5}$,则sin(α+$\frac{π}{4}$)=$\frac{3}{5}$,
又α∈($\frac{π}{4}$,$\frac{3π}{4}$),
∴α+$\frac{π}{4}$∈($\frac{π}{2}$,π),
∴cos(α+$\frac{π}{4}$)=-$\frac{4}{5}$
因此,cos=cos[(α+$\frac{π}{4}$)-$\frac{π}{4}$]=cos(α+$\frac{π}{4}$)cos$\frac{π}{4}$+sin(α+$\frac{π}{4}$)sin$\frac{π}{4}$=-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$+$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{10}$.
点评 本题考查了正弦函数的图象,熟记公式的解题的关键,难度不大,属于基础题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | 20 种 | B. | 40 种 | C. | 42种 | D. | 48种 |
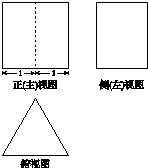
| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
| A. | 充分必要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |

| A. | T4=53×${C}_{9}^{3}$ | B. | T6=-55×${C}_{9}^{5}$ | C. | T5=74×${C}_{9}^{4}$ | D. | T4=-73×${C}_{9}^{3}$ |