题目内容
15.将函数y=sin($2x-\frac{π}{3})$的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根据函数y=Asin(ωx+φ)的图象变换规律,变换后所得函数的解析式为y=sin(2x+2ϕ-$\frac{π}{3}$],再由它是奇函数,可得2ϕ-$\frac{π}{3}$=kπ,k∈z,由此求得ϕ的最小值.
解答 解:将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移ϕ(ϕ>0)个单位后,
所得到的图象对应的函数解析式为y=sin[2(x+ϕ)-$\frac{π}{3}$]=sin(2x+2ϕ-$\frac{π}{3}$],
再由y=sin(2x+2ϕ-$\frac{π}{3}$]为奇函数,可得2ϕ-$\frac{π}{3}$=kπ,k∈z,则ϕ的最小值为$\frac{π}{6}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的奇偶性,属于中档题.

练习册系列答案
相关题目
5.某人捡到不规则形状的五面体石块,他在每个面上作了记号,投掷了100次,并且记录了每个面落在桌面上的次数(如表),如果再投掷一次,请估计石块的第4面落在桌面上的概率是多少?
| 石块的面 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 32 | 18 | 15 | 13 | 22 |
6.已知集合A={x|x2+2x-3<0},B={x|-$\sqrt{2}$<x<1},则A∩B等于( )
| A. | Φ | B. | {x|-3<x<1} | C. | {x|-$\sqrt{2}$<x<1} | D. | {x|x2+2x-3<0} |
20.已知定义在R的函数f(x)满足:
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |
4.执行如图所示的程序框图,若输出实数k的值为4,则框图中x的值是( )
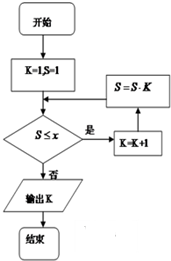

| A. | 4 | B. | 16 | C. | 24 | D. | 120 |