题目内容
9.为了得到函数y=3cos2x的图象,只需把函数$y=3sin(2x+\frac{π}{6})$的图象上所有的点( )| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
分析 由条件利用y=Asin(ωx+φ)的图象变换规律、诱导公式,可得结论.
解答 解:把函数$y=3sin(2x+\frac{π}{6})$的图象上所有的向左平移$\frac{π}{6}$个单位,
可得函数y=3sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=3sin(2x+$\frac{π}{2}$)=3cos2x的图象,
故选:D.
点评 本题主要考查诱导公式的应用,利用了y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
20.已知定义在R的函数f(x)满足:
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
①f(-x)=f(x);
②f(x-2)=f(x);
③?x1,x2∈[0,1](x1≠x2),$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}$>0.
则( )
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |
19.已知{an}是公比q>0的等比数列,a1+a2+a3=26,a5+a6+a7=2106,则首项a1=( )
| A. | 1 | B. | 2 | C. | $\frac{2}{7}$ | D. | $\frac{2}{3}$ |
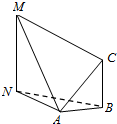 如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.
如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.