题目内容
已知数列{an}的通项公式为an=pn+q,其中p,q是常数,且p≠0.
(Ⅰ)数列{an}是否一定是等差数列?如果是,其首项与公差是什么?
(Ⅱ)设数列{an}的前n项和为Sn,且S10=310,S20=1220,试确定an的公式.
(Ⅰ)数列{an}是否一定是等差数列?如果是,其首项与公差是什么?
(Ⅱ)设数列{an}的前n项和为Sn,且S10=310,S20=1220,试确定an的公式.
(Ⅰ)∵an=pn+q,
∴an+1-an=[p(n+1)+q]-(pn+q)=pn+p+q-pn-q=p,
∴{an}是等差数列,且公差为p.
在通项公式中令n=1,得a1=p+q,
∴这个等差数列的首项是p+q,公差是p;
(Ⅱ)由(Ⅰ)知{an}是等差数列,S10=310,S20=1220,将它们代入公式Sn=
=
=
,
得
⇒
∴an=6n-2.
∴an+1-an=[p(n+1)+q]-(pn+q)=pn+p+q-pn-q=p,
∴{an}是等差数列,且公差为p.
在通项公式中令n=1,得a1=p+q,
∴这个等差数列的首项是p+q,公差是p;
(Ⅱ)由(Ⅰ)知{an}是等差数列,S10=310,S20=1220,将它们代入公式Sn=
| n(a1+an) |
| 2 |
| n[(p+q)+(pn+q)] |
| 2 |
| n(pn+p+2q) |
| 2 |
得
|
|
∴an=6n-2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
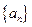 是一个公差为
是一个公差为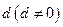 的等差数列,它的前
的等差数列,它的前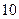 项和
项和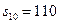 且
且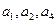 成等比数列,(1)证明
成等比数列,(1)证明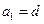 ;(2)求公差
;(2)求公差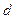 的值和数列
的值和数列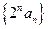 的前
的前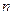 项和
项和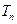 .
.