题目内容
等差数列{an}中的a1，a7是函数f（x）=
x3-4x2+6x-1的极值点，则log2a4=（ ）
| 1 |
| 3 |
| A．2 | B．3 | C．4 | D．5 |
∵a1，a7是函数f（x）=
x3-4x2+6x-1的极值点，
∴a1，a7是导函数方程f′（x）=0的两根，
对函数求导数可得f′（x）=x2-8x+6，
∴a1，a7为方程x2-8x+6=0的两根，
由韦达定理可得a1+a7=8，
由等差数列的性质可得log2a4=log2
=2
故选：A
| 1 |
| 3 |
∴a1，a7是导函数方程f′（x）=0的两根，
对函数求导数可得f′（x）=x2-8x+6，
∴a1，a7为方程x2-8x+6=0的两根，
由韦达定理可得a1+a7=8，
由等差数列的性质可得log2a4=log2
| a1+a7 |
| 2 |
故选：A
练习册系列答案
阅读快车系列答案
相关题目
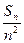，如果存在正整数M，使得对一切正整数n，Tn≤M都成立．则M的最小值是__________．