题目内容
20.已知函数f(x)=$\sqrt{3}$sin2x+2+2cos2x,求f(x)的最小正周期与单调递减区间.分析 利用三角恒等变换化简函数的解析式,再根据正弦函数的周期性和单调性求得f(x)的最小正周期与单调递减区间.
解答 解:函数f(x)=$\sqrt{3}$sin2x+2+2cos2x=$\sqrt{3}$sin2x+cos2x+3=2sin(2x+$\frac{π}{6}$)+3,
显然它的最小正周期为$\frac{2π}{2}$=π.
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得 kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,k∈z,
故函数的减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈z.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
16.下列命题中,真命题是( )
| A. | ?x0∈R,使得e0≤0 | B. | sin2x+$\frac{2}{sinx}$≥3(x≠kπ,k∈Z) | ||
| C. | 函数f(x)=2x-x2有两个零点 | D. | a>1,b>1是ab>1的充分不必要条件 |
17.设f(x)是定义在R上的恒不为零的函数,对?x,y∈R,都有f(x)•f(y)=f(x+y),若数列{an}满足a1=$\frac{1}{3},{a_n}=f(n),n∈{N^*}$,且其前n项和Sn对任意的正整数n都有Sn≤M成立,则M的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
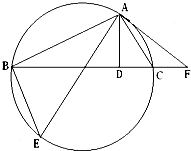 如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.
如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.