题目内容
16.下列命题中,真命题是( )| A. | ?x0∈R,使得e0≤0 | B. | sin2x+$\frac{2}{sinx}$≥3(x≠kπ,k∈Z) | ||
| C. | 函数f(x)=2x-x2有两个零点 | D. | a>1,b>1是ab>1的充分不必要条件 |
分析 对于A,根据指数函数恩对性质即可判断,
对于B.根据基本不等式,需要sinx>0,即可判断,
对于C.根据图象即可判断,
对于D,根据充分和必要条件即可判断.
解答 解:对于A.∵?x∈R,都有ex>0,故A为假命题;
对于B.sin2x+$\frac{2}{sinx}$=sin2x+$\frac{1}{sinx}$+$\frac{1}{sinx}$≥3,若成立,需要sinx>0,故B为假命题,
对于C.f(x)=f(x)=2x-x2=0,分别画出y=x2与y=2x的图象,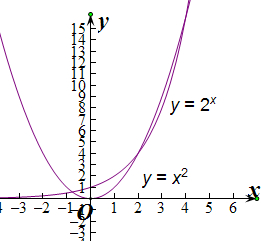
由图象可知有3个交点,故有3个零点,解得x=±$\sqrt{2}$,故C为假命题,
对于D.a>1,b>1一定能推出ab>1,但是当a=-2,b=-2时,ab>1,故a>1,b>1是ab>1的充分不必要条件为真命题.
故选:D
点评 本题主要考查了命题的判断,涉及了函数的性质,零点的求法,基本不等式等知识,属于中档题.

练习册系列答案
相关题目
4. 棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )
棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )
 棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )
棱长是1的正四面体PABC的四个顶点都在球O的表面上,若M、N分别是棱CA、CB的中点,则△PMN所在的平面截球O所得的截面面积是( )| A. | $\frac{2}{11}π$ | B. | $\frac{4}{11}π$ | C. | $\frac{8}{11}π$ | D. | $\frac{16}{11}π$ |
5.一名射击运动员对靶射击,直到第一次命中为止,若每次命中的概率是0.6,且各次射击结果互不影响,现在有4颗子弹,则命中后剩余子弹数X的均值为( )
| A. | 2.44 | B. | 3.376 | C. | 2.376 | D. | 2.4 |
 从某班的科技创新比赛结果中任抽取9名学生的成绩,其分布如茎叶图所示:
从某班的科技创新比赛结果中任抽取9名学生的成绩,其分布如茎叶图所示: 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.