题目内容
15.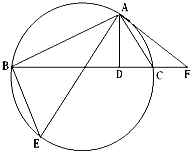 如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.
如图,AD是△ABC的高,AE是△ABC的外接圆的直径,过点A作圆的切线交BC的延长线于点F.(1)求证:△ABE∽△ADC;
(2)若BD=4CD=4CF=8,求△ABC的外接圆的半径.
分析 (1)证明三角形中两对对应角相等,即可证明结论;
(2)利用切割线定理,结合三角形相似的性质,即可求△ABC的外接圆的半径.
解答 (1)证明:∵AE是直径,∴$∠ABE=\frac{π}{2}=∠ADC$…(1分)
又∵∠AEB=∠ACD…(2分)
∴△ABE∽△ADC…(4分)
(2)解:∵过点A作圆的切线交BC的延长线于点F,
∴AF2=FC•FB
∴FA=2$\sqrt{6}$,…(5分)
∴AD=2$\sqrt{2}$…(7分)
∴AC=2$\sqrt{3}$ …(8分)
∴AB=6$\sqrt{2}$,…(9分)
由(1)得$\frac{AB}{AE}=\frac{AD}{AC}$
∴AE=6$\sqrt{3}$
∴△ABC的外接圆的半径为3$\sqrt{3}$.…(10分)
点评 本题考查三角形相似的判定与性质,考查切割线定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.函数f(x)=$\frac{2co{s}^{2}(x-1)-x}{x-1}$,其图象的对称中心是( )
| A. | (-1,1) | B. | (1,-1) | C. | (0,1) | D. | (0,-1) |
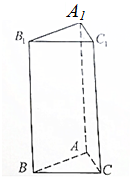 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,底面ABC为正三角形,AA1=4,BC=2,延长AB至D,使BD=AB.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,底面ABC为正三角形,AA1=4,BC=2,延长AB至D,使BD=AB.