题目内容
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.
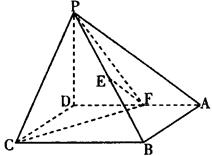
(Ⅰ)求证:EF⊥平面PBC;
(Ⅱ)求二面角F-PC-B的平面角的余弦值.

(Ⅰ)求证:EF⊥平面PBC;
(Ⅱ)求二面角F-PC-B的平面角的余弦值.
(Ⅰ)见解析 (Ⅱ)

(I)根据线面垂直的判定定理,只须证明 ,
,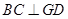 从而证明出
从而证明出 平面
平面 ,然后证明出GD//EF,问题到此基本得以解决.
,然后证明出GD//EF,问题到此基本得以解决.
(II)关键是作出二面角的平面角,连结 ,易证:
,易证:

 ,
,

 ,所以
,所以 是二面角
是二面角 的平面角,然后解三角形求角即可
的平面角,然后解三角形求角即可
(Ⅰ)取 的中点
的中点 ,连结
,连结 ,
,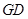 则
则 //
// ,且
,且 ,
,

又∵ //
// ,且
,且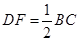 ,∴
,∴ //
// 且
且 ,∴四边形
,∴四边形 为平行四边形,∴
为平行四边形,∴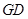 //
// .……………………… 3分
.……………………… 3分
由于 平面
平面 ,∴
,∴ ,又
,又 ,∴
,∴ 平面
平面 ,又
,又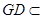 平面
平面 ,∴
,∴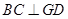 ,在等腰直角三角形
,在等腰直角三角形 中,由
中,由 为
为 中点,∴
中点,∴ ,
,
 ,∴
,∴ 平面
平面 , ……………………………………………… 5分
, ……………………………………………… 5分
∵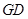 //
// ,∴
,∴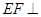 平面
平面 . ………………………………………………… 6分
. ………………………………………………… 6分
(Ⅱ)连结 ,∵
,∵ ,
, //
// ,∴
,∴

 , ∵
, ∵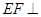 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 平面
平面 ,
,


 , ∴
, ∴ 是二面角
是二面角 的平面角.…………… 9分
的平面角.…………… 9分
在 中,
中,
 ,
, ,
,
 ,所以二面角
,所以二面角 的平面角的余弦值为
的平面角的余弦值为
 ,
,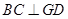 从而证明出
从而证明出 平面
平面 ,然后证明出GD//EF,问题到此基本得以解决.
,然后证明出GD//EF,问题到此基本得以解决.(II)关键是作出二面角的平面角,连结
 ,易证:
,易证:

 ,
,

 ,所以
,所以 是二面角
是二面角 的平面角,然后解三角形求角即可
的平面角,然后解三角形求角即可(Ⅰ)取
 的中点
的中点 ,连结
,连结 ,
,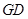 则
则 //
// ,且
,且 ,
,
又∵
 //
// ,且
,且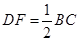 ,∴
,∴ //
// 且
且 ,∴四边形
,∴四边形 为平行四边形,∴
为平行四边形,∴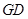 //
// .……………………… 3分
.……………………… 3分由于
 平面
平面 ,∴
,∴ ,又
,又 ,∴
,∴ 平面
平面 ,又
,又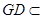 平面
平面 ,∴
,∴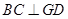 ,在等腰直角三角形
,在等腰直角三角形 中,由
中,由 为
为 中点,∴
中点,∴ ,
, ,∴
,∴ 平面
平面 , ……………………………………………… 5分
, ……………………………………………… 5分∵
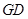 //
// ,∴
,∴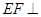 平面
平面 . ………………………………………………… 6分
. ………………………………………………… 6分(Ⅱ)连结
 ,∵
,∵ ,
, //
// ,∴
,∴

 , ∵
, ∵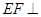 平面
平面 ,∴
,∴ ,
, ,∴
,∴ 平面
平面 ,
,


 , ∴
, ∴ 是二面角
是二面角 的平面角.…………… 9分
的平面角.…………… 9分在
 中,
中,
 ,
, ,
, ,所以二面角
,所以二面角 的平面角的余弦值为
的平面角的余弦值为

练习册系列答案
相关题目
 中,二面角
中,二面角 的余弦值为 .
的余弦值为 . 所成的角为300,则它和平面
所成的角为300,则它和平面 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 ,则这样的直线
,则这样的直线 各棱长均为1,
各棱长均为1, 分别在棱
分别在棱 上,且
上,且 ,则直线
,则直线 与直线
与直线 所成角的正切值的取值范围是
所成角的正切值的取值范围是 
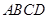 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,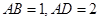 ,
,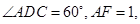
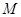 是线段
是线段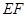 的中点.
的中点.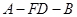 的正弦值;
的正弦值;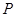 为一动点,若点
为一动点,若点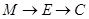 的路线运动到点
的路线运动到点 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥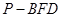 的体积的最小值.
的体积的最小值.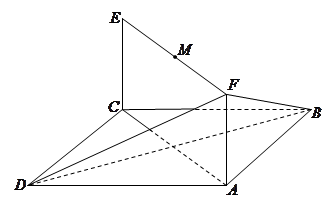
 与这三条直线所成的角均为
与这三条直线所成的角均为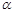 ,则
,则 .
.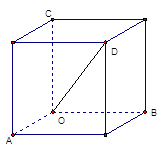
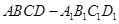 中,异面直线
中,异面直线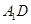 与
与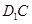 所成的角为_______度;直线
所成的角为_______度;直线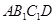 所成的角为_______度.
所成的角为_______度.