题目内容
已知直线 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 作与
作与 、
、 所成的角都是45°的直线
所成的角都是45°的直线 ,则这样的直线
,则这样的直线 可作( )条
可作( )条
 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 作与
作与 、
、 所成的角都是45°的直线
所成的角都是45°的直线 ,则这样的直线
,则这样的直线 可作( )条
可作( )条 | A.2 | B.3 | C.4 | D.无数 |
A
解:因为直线 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 作与
作与 、
、 所成的角都是45°的直线
所成的角都是45°的直线 ,则这样的直线
,则这样的直线 可作2条,选A
可作2条,选A
 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 作与
作与 、
、 所成的角都是45°的直线
所成的角都是45°的直线 ,则这样的直线
,则这样的直线 可作2条,选A
可作2条,选A
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
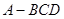 中,面
中,面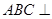 面
面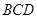 ,
,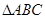 是正三角形,
是正三角形, 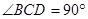 ,
,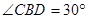 .
.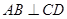 ;
;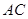 与
与 所成角的余弦值.
所成角的余弦值.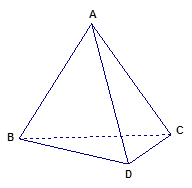
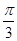 ,π);
,π);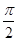 ;
;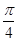 的直线有3条;
的直线有3条;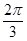 ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成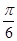 的直线有3条.
的直线有3条.



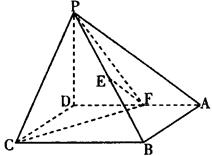
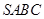 中,各边及对角线长都相等,若
中,各边及对角线长都相等,若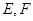 分别为
分别为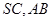 的中点,那么异面直线
的中点,那么异面直线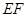 与
与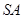 所成的角等于( )
所成的角等于( )


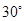
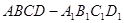 中,AB=BC=2,
中,AB=BC=2,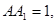 则
则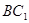 与面
与面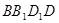 所成角的正弦值为( )
所成角的正弦值为( )

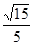

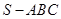 中,平面
中,平面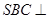 平面
平面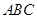 ,
,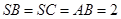 ,
,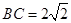 ,
,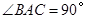 ,
,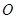 为
为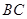 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面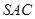 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角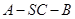 的余弦值.
的余弦值.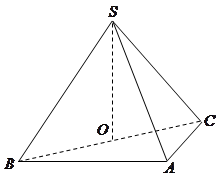
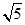 ,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )
,底面ABCD是边长为2的正方形,则CD与PA所成角的余弦值为( )


