题目内容
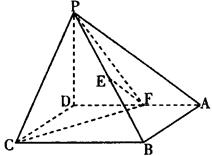
如图,已知平行四边形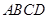 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,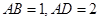 ,
,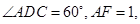
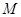 是线段
是线段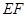 的中点.
的中点.
(Ⅰ)求二面角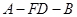 的正弦值;
的正弦值;
(Ⅱ)设点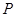 为一动点,若点
为一动点,若点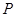 从
从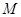 出发,沿棱按照
出发,沿棱按照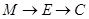 的路线运动到点
的路线运动到点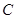 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥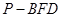 的体积的最小值.
的体积的最小值.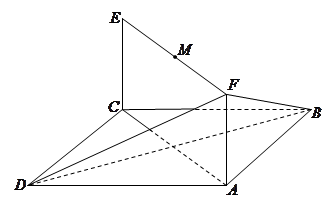
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,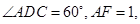
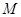 是线段
是线段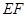 的中点.
的中点.(Ⅰ)求二面角
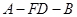 的正弦值;
的正弦值;(Ⅱ)设点
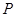 为一动点,若点
为一动点,若点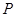 从
从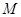 出发,沿棱按照
出发,沿棱按照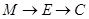 的路线运动到点
的路线运动到点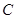 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥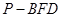 的体积的最小值.
的体积的最小值.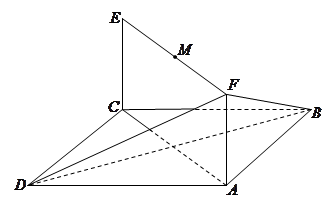
(Ⅰ)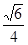
(Ⅱ) .
.
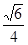
(Ⅱ)
 .
.(I)可采用传统方法作出二面角的平面角,求出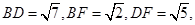 后,可知
后,可知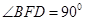 ,过
,过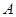 作
作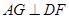 于
于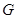 ,又过
,又过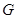 作
作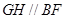 交
交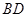 于
于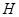 ,连结
,连结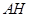 .则易证
.则易证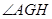 为二面角
为二面角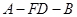 的平面角.然后解
的平面角.然后解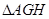 即可.
即可.
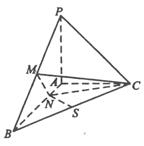
(2)解本小题的关键是确定点P的位置.设AC与BD交于O,则OF//CM,所以CM//平面FBD,所以M与C到平面BFD的距离相等,当P点在M或C时,三棱锥P—BFD的体积的最小.
(Ⅰ)法一:易求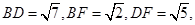 由勾股定理知
由勾股定理知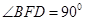 ,
,
设点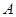 在面
在面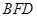 内的射影为
内的射影为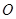 ,过
,过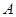 作
作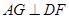 于
于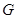 ,连结
,连结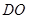 ,
,
则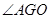 为二面角
为二面角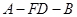 的平面角. ………………3分
的平面角. ………………3分
在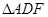 中由面积法易求
中由面积法易求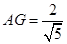 ,………………5分
,………………5分
由体积法求得点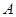 到面
到面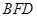 的距离是
的距离是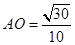 ,所以
,所以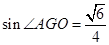 ,
,
所以求二面角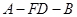 的大小正弦值为
的大小正弦值为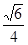 ………………7分
………………7分
法二:易求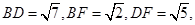 由勾股定理知
由勾股定理知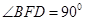 ,
,
过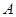 作
作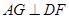 于
于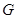 ,又过
,又过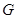 作
作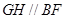 交
交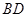 于
于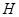 ,连结
,连结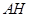 .
.
则易证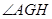 为二面角
为二面角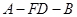 的平面角………………2分
的平面角………………2分
在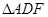 中由面积法易求
中由面积法易求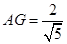 ,
,
从而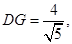 于是
于是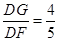 ,所以
,所以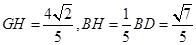 ,………3分
,………3分
在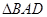 中由余弦定理求得
中由余弦定理求得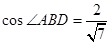 .………………4分
.………………4分
再在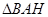 中由余弦定理求得
中由余弦定理求得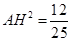 .………………5分
.………………5分
最后在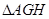 中由余弦定理求得
中由余弦定理求得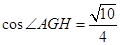 ,………………6分
,………………6分
所以求二面角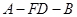 的大小正弦值为
的大小正弦值为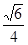 ………………7分
………………7分
(Ⅱ)设AC与BD交于O,则OF//CM,………………8分
所以CM//平面FBD,………………9分
当P点在M或C时,三棱锥P—BFD的体积的最小. ……………10分
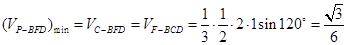 .
.
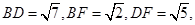 后,可知
后,可知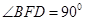 ,过
,过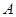 作
作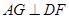 于
于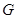 ,又过
,又过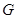 作
作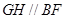 交
交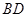 于
于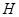 ,连结
,连结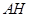 .则易证
.则易证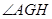 为二面角
为二面角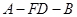 的平面角.然后解
的平面角.然后解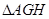 即可.
即可.(2)解本小题的关键是确定点P的位置.设AC与BD交于O,则OF//CM,所以CM//平面FBD,所以M与C到平面BFD的距离相等,当P点在M或C时,三棱锥P—BFD的体积的最小.
(Ⅰ)法一:易求
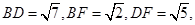 由勾股定理知
由勾股定理知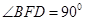 ,
,设点
 在面
在面 内的射影为
内的射影为 ,过
,过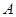 作
作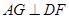 于
于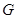 ,连结
,连结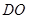 ,
,则
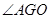 为二面角
为二面角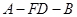 的平面角. ………………3分
的平面角. ………………3分在
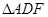 中由面积法易求
中由面积法易求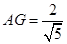 ,………………5分
,………………5分由体积法求得点
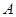 到面
到面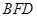 的距离是
的距离是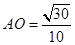 ,所以
,所以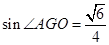 ,
,所以求二面角
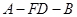 的大小正弦值为
的大小正弦值为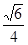 ………………7分
………………7分法二:易求
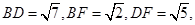 由勾股定理知
由勾股定理知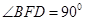 ,
,过
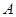 作
作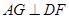 于
于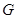 ,又过
,又过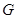 作
作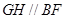 交
交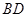 于
于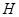 ,连结
,连结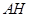 .
.则易证
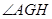 为二面角
为二面角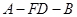 的平面角………………2分
的平面角………………2分在
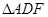 中由面积法易求
中由面积法易求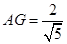 ,
,从而
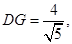 于是
于是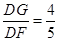 ,所以
,所以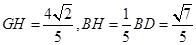 ,………3分
,………3分在
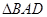 中由余弦定理求得
中由余弦定理求得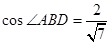 .………………4分
.………………4分再在
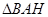 中由余弦定理求得
中由余弦定理求得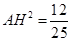 .………………5分
.………………5分最后在
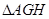 中由余弦定理求得
中由余弦定理求得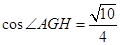 ,………………6分
,………………6分所以求二面角
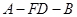 的大小正弦值为
的大小正弦值为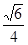 ………………7分
………………7分(Ⅱ)设AC与BD交于O,则OF//CM,………………8分
所以CM//平面FBD,………………9分
当P点在M或C时,三棱锥P—BFD的体积的最小. ……………10分
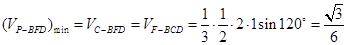 .
.
练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 中,
中, =2
=2 ,
, =
= ,则二面角
,则二面角 的大小是 ( )
的大小是 ( )



 中,AB=BC=2,
中,AB=BC=2, 则
则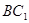 与面
与面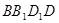 所成角的正弦值为( )
所成角的正弦值为( )

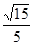

 中,
中, 是
是 中点,
中点,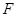 是
是 的中点,则直线
的中点,则直线 与
与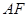 所成角的大小为_______.
所成角的大小为_______.
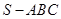 中,平面
中,平面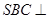 平面
平面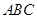 ,
,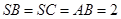 ,
,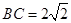 ,
,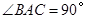 ,
,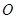 为
为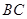 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面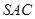 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角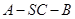 的余弦值.
的余弦值.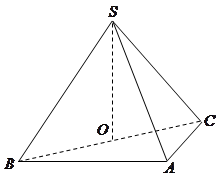
 中,
中, 与平面
与平面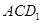 所成的角的余弦值是( )
所成的角的余弦值是( )


