题目内容
4.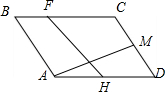 如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.
如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.(1)用$\overrightarrow{a}$,$\overrightarrow{b}$来表示$\overrightarrow{AM}$,$\overrightarrow{HF}$;
(2)若|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,求$\overrightarrow{AM}$•$\overrightarrow{HF}$.
分析 (1)M是DC的中点,且$\overrightarrow{DM}$与$\overrightarrow{AB}$同向,所以根据共线向量基本定理有$\overrightarrow{DM}$=$\frac{1}{2}$$\overrightarrow{AB}$=$\frac{1}{2}\overrightarrow{a}$,所以$\overrightarrow{AM}$=$\overrightarrow{AD}$+$\overrightarrow{DM}$=$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{a}$,同样可求出$\overrightarrow{HF}$;
(2)运用向量的数量积的定义可得$\overrightarrow{a}$•$\overrightarrow{b}$=-6,再由向量数量积的性质即可求得所求值.
解答 解:(1)$\overrightarrow{AM}$=$\overrightarrow{AD}$+$\overrightarrow{DM}$=$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{a}$;
$\overrightarrow{HF}$=$\overrightarrow{HD}$+$\overrightarrow{DC}$+$\overrightarrow{CF}$=$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$-$\frac{2}{3}\overrightarrow{b}$=$\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$;
(2)若|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$,
则$\overrightarrow{a}$•$\overrightarrow{b}$=3×4cos$\frac{2π}{3}$=-6,
则有$\overrightarrow{AM}$•$\overrightarrow{HF}$=($\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{a}$)•($\overrightarrow{a}$-$\frac{1}{6}$$\overrightarrow{b}$)=$\frac{1}{2}$${\overrightarrow{a}}^{2}$-$\frac{1}{6}$${\overrightarrow{b}}^{2}$+$\frac{11}{12}$$\overrightarrow{a}•\overrightarrow{b}$
=$\frac{1}{2}×$9-$\frac{1}{6}$×16-$\frac{11}{12}$×6=-$\frac{11}{3}$.
点评 本题考查向量的加法运算,及共线向量基本定理和向量的数量积的定义和性质,考查运算能力,属于中档题.

 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案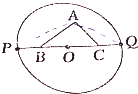 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
 已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$
已知函数f(x)=$\left\{\begin{array}{l}{x,x∈[0,2]}\\{\frac{4}{x},x∈(2,4]}\end{array}\right.$ 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别F1、F2,动直线l与椭圆相切于点P,作F1A,F2B垂直于直线l,垂足分别为A,B,记λ=$\frac{B{F}_{2}}{A{F}_{1}}$.当P为左顶点时,λ=9,且λ=1时,四边形AF1F2B的周长为22.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别F1、F2,动直线l与椭圆相切于点P,作F1A,F2B垂直于直线l,垂足分别为A,B,记λ=$\frac{B{F}_{2}}{A{F}_{1}}$.当P为左顶点时,λ=9,且λ=1时,四边形AF1F2B的周长为22.