题目内容
16．
如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别F1、F2，动直线l与椭圆相切于点P，作F1A，F2B垂直于直线l，垂足分别为A，B，记λ=$\frac{B{F}_{2}}{A{F}_{1}}$．当P为左顶点时，λ=9，且λ=1时，四边形AF1F2B的周长为22．（1）试确定椭圆的标准方程；
（2）求证：BF2•AF1为定值．
分析 （1）通过当P为左顶点时λ=9及PF2-PF1=2c，得4a=5c，再通过λ=1时四边形AF1F2B的周长为22，可知b+2c=11，计算即可；
（2）设直线l与坐标轴的交点分别为M（m，0），N（0，n），（m、n＞0），通过直线l的方程nx+my-mn=0，可得BF2=$\frac{|4n-mn|}{\sqrt{{m}^{2}+{n}^{2}}}$，AF1=$\frac{4n+mn}{\sqrt{{m}^{2}+{n}^{2}}}$，再利用直线l与椭圆相切，即9m2+9n2+16n2-m2n2=0，可得BF2•AF1=9．
解答 （1）解：当P为左顶点时，λ=9，即PF2=9PF1，
又∵PF2-PF1=2c，∴c=4PF1=4a-4c，即4a=5c，
当λ=1时，四边形AF1F2B的周长为22，
即2b+4c=22，∴b+2c=11，
又∵a2-b2=c2，∴a=5，b=3，c=4，
∴椭圆的标准方程为：$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$；
（2）证明：由（1）知F1（-4，0），F2（4，0），
设直线l与坐标轴的交点分别为M（m，0），N（0，n），（m、n＞0），
则直线l的方程为：nx+my-mn=0，
∴BF2=$\frac{|4n-mn|}{\sqrt{{m}^{2}+{n}^{2}}}$，AF1=$\frac{4n+mn}{\sqrt{{m}^{2}+{n}^{2}}}$，
联立直线l与椭圆方程，消去y得：$（9+\frac{25{n}^{2}}{{m}^{2}}）{x}^{2}$-$\frac{50{n}^{2}}{m}x$+25n2-225=0，
∵直线l与椭圆相切，∴△=$（\frac{50{n}^{2}}{m}）^{2}$-$4×（9+\frac{25{n}^{2}}{{m}^{2}}）（25{n}^{2}-225）$=0，
化简，得9m2-m2n2+25n2=0，即9m2+9n2+16n2-m2n2=0，
∴BF2•AF1=$\frac{|4n-mn|}{\sqrt{{m}^{2}+{n}^{2}}}$•$\frac{4n+mn}{\sqrt{{m}^{2}+{n}^{2}}}$=$\frac{|16{n}^{2}-{m}^{2}{n}^{2}|}{{m}^{2}+{n}^{2}}$=9．
点评 本题考查椭圆的简单性质，直线与椭圆的位置关系，点到直线的距离公式，注意解题方法的积累，属于难题．
名题金卷系列答案| A． | 6$\overrightarrow{a}$+2$\overrightarrow{b}$ | B． | $\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C． | $\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ | D． | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
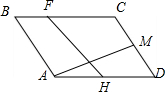如图，平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，H、M是AD、DC的中点，BF=$\frac{1}{3}$BC．
| A． | f（x）=x2 | B． | f（x）=sinx | C． | f（x）=ex | D． | f（x）=$\frac{1}{x}$ |