题目内容
14.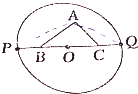 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
分析 利用余弦定理,求出|AP|2、|AQ|2,结合∠AOP+∠AOQ=180°,即可求|AP|2+|AQ|2+|PQ|2的值.
解答 解:由题意,OA=OB=1,OP=OQ=n
△AOP中,根据余弦定理AP2=OA2+OP2-2OA•OPcos∠AOP
同理△AOQ中,AQ2=OA2+OQ2-2OA•OQcos∠AOQ
因为∠AOP+∠AOQ=180°,
所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2+2n2+(2n)2=2+6n2为定值.
点评 本题考查直线与圆的位置关系,考查余弦定理的运用,考查学生的计算能力,属于基础题.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
5.设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )
| A. | $\root{3}{4V}$ | B. | $\root{3}{6V}$ | C. | $\root{3}{8V}$ | D. | $\sqrt{4V}$ |
19. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
3.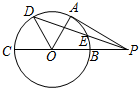 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{3\sqrt{7}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
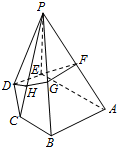 如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.
如图所示,在五棱锥P-ABCDE中,PE⊥平面ABCDE,DE⊥AE,AB∥DE,BC∥AE.AE=AB=PE=2DE=2BC,F为棱PA的中点,过D、E、F的平面α与棱PB、PC分别交于点G、H.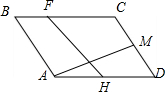 如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.
如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.