题目内容
16.已知函数f(x)=x2+x,x∈R,若a、b、c∈R,且a+b>0,b+c>0,c+a>0,则f(a)+f(b)+f(c)的值的符号为( )| A. | 正 | B. | 负 | C. | 零 | D. | 不确定 |
分析 根据解析式得出f(a)+f(b)+f(c)=(a2+b2+c2)+(a+b+c),运用不等式的性质得出2(a+b+c)>0,判断即可得出答案.
解答 解:∵函数f(x)=x2+x,x∈R,
∴f(a)=a2+a,f(b)=b2+b,f(c)=c2+c,
∴f(a)+f(b)+f(c)=(a2+b2+c2)+(a+b+c),
∵a、b、c∈R,且a+b>0,b+c>0,c+a>0,
∴2(a+b+c)>0,
即(a2+b2+c2)+(a+b+c)>0,
∴f(a)+f(b)+f(c)的值的符号为正数,
故选;A.
点评 本题考查了函数值的运用,不等式的性质,判定符合问题,属于容易题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知函数f(x)=$\frac{1}{{3}^{x}-1}$+a,若f(x)是奇函数,则a=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}+1$ |
8.某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )


| A. | f(x)=x2 | B. | f(x)=sinx | C. | f(x)=ex | D. | f(x)=$\frac{1}{x}$ |
6.如图所示,在复平面内,点A对应的复数为z,则复数z2等于( )


| A. | 3-4i | B. | 3+4i | C. | -3+4i | D. | -3-4i |
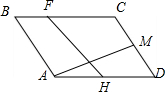 如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.
如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.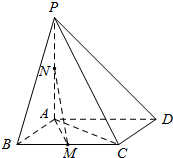 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$. 如图,阴影部分(包括边界)为平面区域D,若点P(x,y)在区域D内,则z=x+2y的最小值是-1;x,y满足的约束条件是$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.
如图,阴影部分(包括边界)为平面区域D,若点P(x,y)在区域D内,则z=x+2y的最小值是-1;x,y满足的约束条件是$\left\{\begin{array}{l}2x-y+2≥0\\ x≤0\\ y≥0.\end{array}\right.$.