题目内容
9.数列{an}的通项公式为an=$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n+1}$,若对任意的n∈N*,都有$\frac{11}{6}$log(a-1)a-$\frac{11}{3}$loga(a-1)>an,求实数a的取值范围.分析 由题意化简an+1-an后,根据符号判断出数列{an}的单调性,并求出它的最大项,利用对数的运算将恒成立的不等式化简,利用底数的范围求出a的范围,再根据对数函数的单调性对底数分类讨论,分别利用对数函数的单调性列出关于a的不等式,利用构造函数法和导数求出实数a的取值范围.
解答 解:因为an=$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n+1}$,
所以an+1-an=($\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n+1}$+$\frac{1}{2n+2}$+$\frac{1}{2n+3}$)-($\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n+1}$)
=$\frac{1}{2n+2}$+$\frac{1}{2n+3}$-$\frac{1}{n}$=$\frac{-5n-6}{n(2n+2)(2n+3)}$<0,
则an+1<an,即数列{an}是递减数列,最大项是a1=1$+\frac{1}{2}+\frac{1}{3}$=$\frac{11}{6}$,
因为对任意的n∈N*,都有$\frac{11}{6}$log(a-1)a-$\frac{11}{3}$loga(a-1)>an,
所以$\frac{11}{6}$log(a-1)a+$\frac{11}{3}$log(a-1)a>$\frac{11}{6}$,
3log(a-1)a>1=log(a-1)(a-1),①
由$\left\{\begin{array}{l}{a>0且a≠1}\\{a-1>0且a-1≠1}\end{array}\right.$得,a>1且a≠2,
(1)当0<a-1<1时,此时1<a<2,①化为a3<a-1,
设g(a)=a3-a+1,g′(a)=3a2-1,
则当1<a<2时,g′(a)=3a2-1>0,
所以函数g(a)在(1,2)上递增,则g(a)>g(1)=1>0,
所以a3-a+1>0,即a3>a-1在(1,2)上恒成立;
(2)当a-1>1时,此时a>2,①化为a3>a-1,
由(1)可知,函数g(a)在(2,+∞)上递增,则g(a)>g(2)=7>0,
所以a3-a+1>0,即a3>a-1在(2,+∞)上恒成立,
综上可得,实数a的取值范围是(2,+∞).
点评 本题考查数列与不等式相结合,以及构造法、函数与导数的关系的应用,考查分析问题与解决问题的能力,转化思想的应用.

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
| A. | a>1 | B. | a>1或a=-3 | C. | 0<a<1或a=-3 | D. | a>-1 |
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}+1$ |
 如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.
如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.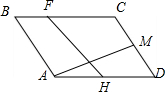 如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.
如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.