题目内容
12.已知函数f(x)=ax(a>0,且a≠1)(1)若a=e,g(x)=mx2,m>0,当函数y=f(x)-g(x)在[-2,4]上有三个不同的零点时,求实数m的取值范围.
(2)若0<a<1,A,B是曲线y=f(x)上不同的两点,点C是弦AB的中点,过点C作x轴的垂线交曲线y=f(x)于点D,设直线AB的斜率为k1,曲线y=f(x)在点D处的切线斜率为k2,求证:k1<k2.
分析 (1)当m>0时,曲线y=f(x)与曲线y=g(x)的公共点个数即方程ex=mx2根的个数.由ex=mx2得$\frac{1}{m}$=$\frac{{x}^{2}}{{e}^{x}}$,设h(x)=$\frac{{x}^{2}}{{e}^{x}}$,h′(x)=$\frac{x(2-x)}{{e}^{x}}$,利用导数研究函数h(x)的单调性,即可得出结论;
(2)根据导数的几何意义,利用导数与曲线切线斜率间的关系证明.
解答 (1)解:当m>0时,曲线y=f(x)与曲线y=g(x)的公共点个数即方程ex=mx2根的个数.
由ex=mx2得$\frac{1}{m}$=$\frac{{x}^{2}}{{e}^{x}}$,
设h(x)=$\frac{{x}^{2}}{{e}^{x}}$,h′(x)=$\frac{x(2-x)}{{e}^{x}}$,
所以在R上不间断的函数h(x)在(-∞,0)上递减,在(0,2)上递增,
在(2,+∞)上递减,
又因为m>0,h(0)=0,h(2)=$\frac{4}{{e}^{2}}$,h(4)=$\frac{16}{{e}^{4}}$,h(-2)=$\frac{4}{{e}^{-2}}$=4e2,
当h(4)≤$\frac{1}{m}$<h(2)时有三公共点,
解得$\frac{{e}^{2}}{4}$<m≤$\frac{{e}^{4}}{16}$;
(2)证明:设A(x1,f(x1)),B(x2,f(x2))(x1<x2)
则k1=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$k2=f′($\frac{{x}_{1}+{x}_{2}}{2}$),
则k1-k2=$\frac{{a}^{{x}_{2}}-{a}^{{x}_{1}}}{{x}_{2}-{x}_{1}}$-${a}^{\frac{{x}_{1}+{x}_{2}}{2}}$lna
=$\frac{{a}^{\frac{{x}_{1}+{x}_{2}}{2}}}{{x}_{2}-{x}_{1}}$[${a}^{\frac{{x}_{2}-{x}_{1}}{2}}$-${a}^{\frac{{x}_{1}-{x}_{2}}{2}}$-(x2-x1)lna],
设$\frac{{x}_{2}-{x}_{1}}{2}$=t>0,L(x)=at-a-t-2tlna,
则L'(x)=lna(at+a-t-2),
当0<a<1时,0<at<1,lna<0
则L'(t)=lna(at+a-t-2)<0,所以L(t)在(0,+∞)递减,
则L(t)<L(0)=0,
又因为$\frac{{a}^{\frac{{x}_{1}+{x}_{2}}{2}}}{{x}_{2}-{x}_{1}}$>0,所以$\frac{{a}^{\frac{{x}_{1}+{x}_{2}}{2}}}{{x}_{2}-{x}_{1}}$[${a}^{\frac{{x}_{2}-{x}_{1}}{2}}$-${a}^{\frac{{x}_{1}-{x}_{2}}{2}}$-(x2-x1)lna]<0,
所以k1-k2<0,
当0<a<1时k1<k2.
点评 本题主要考查利用导数研究函数的单调性、极值、求曲线曲线的斜率等问题,逻辑思维强,考查学生的分析问题,解决问题的能力及运算求解能力,属于难题.

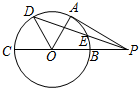 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{3\sqrt{7}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
| A. | 6$\overrightarrow{a}$+2$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
 如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.
如图,四棱锥P-ABCD中,AB,AD,AP两两垂直,长度分别为1,2,2,且$\overrightarrow{DC}$=2$\overrightarrow{AB}$.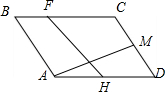 如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.
如图,平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,H、M是AD、DC的中点,BF=$\frac{1}{3}$BC.