题目内容

19．已知函数f（x）=$\left\{\begin{array}{l}{x，x∈[0，2]}\\{\frac{4}{x}，x∈（2，4]}\end{array}\right.$
（1）画出函数f（x）的大致图象；
（2）写出函数f（x）的最大值和单调递减区间．

分析 根据各段解析式画出图象，利用图象，求最大值以及单调区间．

解答 解：（1）已知函数图象如图
（2）由函数图象可知函数的最大值为f（2）=2；
单调递减区间是（2，4]．

点评 本题考查了分段函数图形的画法以及利用图形求函数的性质，比较基础，关键是在画图．

练习册系列答案
相关题目
9．如图所示，在五棱锥P-ABCDE中，PE⊥平面ABCDE，DE⊥AE，AB∥DE，BC∥AE．AE=AB=PE=2DE=2BC，F为棱PA的中点，过D、E、F的平面α与棱PB、PC分别交于点G、H．
（1）求证：DE∥FG；
（2）设DE=1，求三棱锥G-PEF的体积．
10．如图所示，在三棱锥D-ABC中，AB=BC=CD=1，AC=$\sqrt{3}$，平面ACD⊥平面ABC，∠BCD=90°
（1）求证：CD⊥平面ABC；
（2）求直线BD与平面ACD所成角的正弦值．
7．已知单位向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$-k$\overrightarrow{b}$|=$\sqrt{3}$|k$\overrightarrow{a}$+$\overrightarrow{b}$|，其中k＞0，则下列与向量$\overrightarrow{b}$垂直的向量可以是（　　）
A．6$\overrightarrow{a}$+2$\overrightarrow{b}$B．$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$C．$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$D．$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$
14．设函数f（x）=ex-1
（1）当a＞ln2-1且x＞0时，证明：f（x）＞x2-2ax
（2）若f（x）≥x2-ax在（0，1）恒成立，求实数a的取值范围．
4．如图，平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，H、M是AD、DC的中点，BF=$\frac{1}{3}$BC．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$来表示$\overrightarrow{AM}$，$\overrightarrow{HF}$；
（2）若|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=4，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$，求$\overrightarrow{AM}$•$\overrightarrow{HF}$．
11．已知函数f（x）=x3+ax+b（a，b∈R）．
（1）若f（x）的图象在-2≤x≤2部分在x轴的上方，且在点（2，f（2））处的切线与直线9x-y+5=0平行，试求b的取值范围；
（2）当x1，x2∈[0，$\frac{\sqrt{3}}{3}$]，且x1≠x2，不等式|f（x1）-f（x2）|＜|x1-x2|恒成立，求a的取值范围．
8．已知函数f（x）=mx3+3（m-1）x2-m2+1（m＞0）的单调减区间是（0，4），则m=$\frac{1}{3}$．
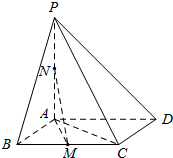11．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，点M，N分别为BC，PA的中点，且AB=AC=1，AD=$\sqrt{2}$．
（Ⅰ）证明：MN∥平面PCD；
（Ⅱ）设直线AC与平面PBC所成角为α，当α在$（0，\frac{π}{6}）$内变化时，求二面角P-BC-A的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网