题目内容
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与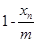 的乘积成正比,比例系数为
的乘积成正比,比例系数为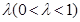 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: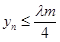 ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
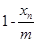 的乘积成正比,比例系数为
的乘积成正比,比例系数为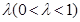 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,(1)证明:
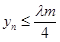 ;
; (2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
(1)详见解析;(2)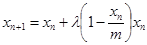 ,证明用数学归纳法,过程详见解析.
,证明用数学归纳法,过程详见解析.
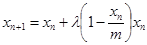 ,证明用数学归纳法,过程详见解析.
,证明用数学归纳法,过程详见解析.试题分析:(1)由已知可得yn是xn的一个二次函数,利用配方法,注意到
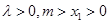 就可证明
就可证明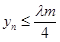 ;(2)由已知有该年的增长量
;(2)由已知有该年的增长量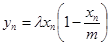 ,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当
,所以第n+1年年初的的数量xn+1=xn+yn,代入即可用 xn表示xn+1;证明草原上的野兔总数量恒小于m,即证对一切非零自然数n,都有xn<m,可考虑用数学归纳法来证明:当n=1时显然成立;再假设当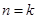 时,命题成立,则对n=k+1时,由于
时,命题成立,则对n=k+1时,由于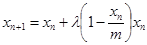 是xk的一个二次函数,结合二次函数的性质,可证
是xk的一个二次函数,结合二次函数的性质,可证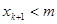 成立,从而有对一切正整数n,
成立,从而有对一切正整数n,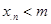 ,即是草原上的野兔总数量恒小于m.
,即是草原上的野兔总数量恒小于m.试题解析:(1)由题意知
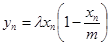 ,配方得:
,配方得: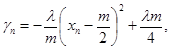 ∵
∵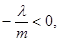 ∴当且仅当
∴当且仅当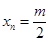 时,
时,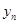 取得最大值
取得最大值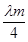 ,即
,即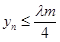 (5分)
(5分) (2)
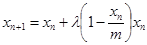 (8分)
(8分)用数列归纳法证明:
当n=1时,由题意知
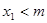 ,故命题成立
,故命题成立假设当
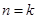 时,命题成立
时,命题成立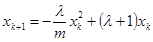 是xk的一个二次函数
是xk的一个二次函数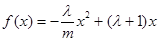 ,
,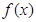 有对称轴
有对称轴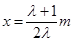 ,开口向下,由
,开口向下,由 ,则
,则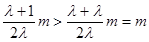 ,于是在
,于是在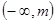 上均有
上均有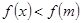 =m
=m取
 ,即知
,即知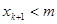 ,∴当
,∴当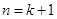 时,命题成立,综上知,对一切正整数n,
时,命题成立,综上知,对一切正整数n,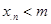 这就是说该草原上的野兔数量不可能无限增长 (13分)
这就是说该草原上的野兔数量不可能无限增长 (13分)
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
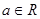 ,函数
,函数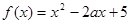 .
.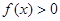 对任意
对任意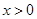 恒成立,求实数
恒成立,求实数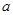 的最值范围;
的最值范围;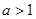 ,且函数
,且函数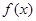 的定义域和值域均为
的定义域和值域均为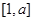 ,求实数
,求实数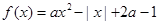 (
(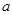 为实常数).
为实常数).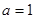 ,求函数
,求函数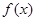 的单调区间;
的单调区间;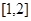 上的最小值为
上的最小值为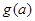 ,求
,求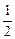 )
)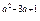 的单调递减区间.
的单调递减区间.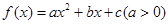 与
与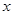 轴的两个交点的横坐标分别为1和3,则不等式
轴的两个交点的横坐标分别为1和3,则不等式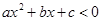 的解集是 .
的解集是 .