题目内容
设x,y∈R,且满足
,则x+y=( )
|
| A.1 | B.2 | C.3 | D.4 |
设f(t)=t3+2t+sint,
则f(t)为奇函数,且f'(t)=3t2+2+cost>0,
即函数f(t)单调递增
由题意可知f(x-2)=-3,f(y-2)=3,
即f(x-2)+f(y-2)=-3+3=0,
即f(x-2)=-f(y-2)=f(2-y),
∵函数f(t)单调递增
∴x-2=2-y,
即x+y=4,
故选:D.
则f(t)为奇函数,且f'(t)=3t2+2+cost>0,
即函数f(t)单调递增
由题意可知f(x-2)=-3,f(y-2)=3,
即f(x-2)+f(y-2)=-3+3=0,
即f(x-2)=-f(y-2)=f(2-y),
∵函数f(t)单调递增
∴x-2=2-y,
即x+y=4,
故选:D.

练习册系列答案
相关题目
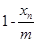 的乘积成正比,比例系数为
的乘积成正比,比例系数为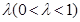 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,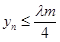 ;
; 
 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值; 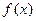 的定义域为
的定义域为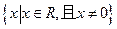 对定义域内的任意
对定义域内的任意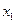 、
、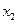 ,都有
,都有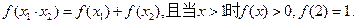
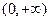 上是增函数;
上是增函数;
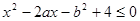 恰有一解,则
恰有一解,则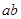 的最大值为______.
的最大值为______.