题目内容
设y=(log2x)2+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,求x的取值范围.
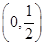 ∪(8,+∞)
∪(8,+∞)解:设y=f(t)=(log2x-1)t+(log2x)2-2log2x+1,
则f(t)是一次函数,当t∈[-2,2]时,
f(t)>0恒成立,则有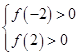
即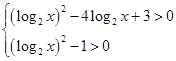
解得log2x<-1或log2x>3.
∴0<x<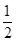 或x>8,
或x>8,
∴x的取值范围是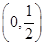 ∪(8,+∞).
∪(8,+∞).
则f(t)是一次函数,当t∈[-2,2]时,
f(t)>0恒成立,则有
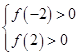
即
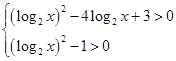
解得log2x<-1或log2x>3.
∴0<x<
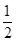 或x>8,
或x>8,∴x的取值范围是
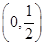 ∪(8,+∞).
∪(8,+∞).
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
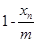 的乘积成正比,比例系数为
的乘积成正比,比例系数为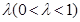 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,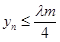 ;
; 
 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值;  的图象过点
的图象过点 和
和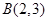 ,则下列各点在函数
,则下列各点在函数



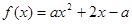 满足
满足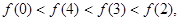 则
则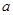 的取值范围为_____
的取值范围为_____ 对
对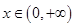 的图象恒在x轴上方,则m的取值范围是( )
的图象恒在x轴上方,则m的取值范围是( )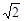 <m<2+2
<m<2+2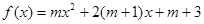 仅有一个负零点,则m的取值范围为( )
仅有一个负零点,则m的取值范围为( )


