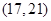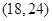题目内容
已知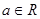 ,函数
,函数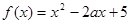 .
.
⑴若不等式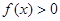 对任意
对任意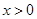 恒成立,求实数
恒成立,求实数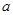 的最值范围;
的最值范围;
⑵若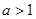 ,且函数
,且函数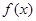 的定义域和值域均为
的定义域和值域均为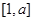 ,求实数
,求实数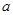 的值.
的值.
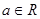 ,函数
,函数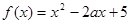 .
.⑴若不等式
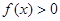 对任意
对任意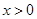 恒成立,求实数
恒成立,求实数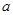 的最值范围;
的最值范围;⑵若
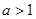 ,且函数
,且函数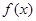 的定义域和值域均为
的定义域和值域均为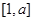 ,求实数
,求实数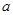 的值.
的值.(1)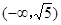 ;(2)
;(2)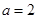 .
.
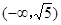 ;(2)
;(2)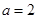 .
.试题分析:(1)根据题意,若不等式
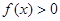 对任意
对任意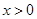 恒成立,参编分离后即可得:
恒成立,参编分离后即可得: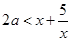 ,从而问题等价于求使
,从而问题等价于求使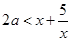 对于任意
对于任意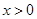 恒成立的
恒成立的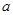 的范围,而
的范围,而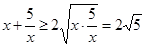 ,当且仅当
,当且仅当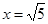 时,“=”成立,故实数
时,“=”成立,故实数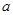 的取值范围是
的取值范围是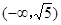 ;(2)由题意可得
;(2)由题意可得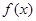 为二次函数,其对称轴为
为二次函数,其对称轴为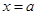 ,因此当
,因此当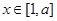 时,可得其值域应为
时,可得其值域应为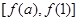 ,从而结合条件
,从而结合条件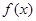 的定义域和值域都是
的定义域和值域都是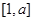 可得关于
可得关于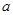 的方程组
的方程组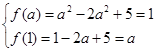 ,即可解得
,即可解得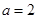 .
.试题解析:(1)∵
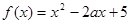 ,∴
,∴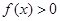 可变形为:
可变形为: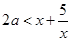 ,而
,而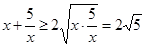 ,当且仅当
,当且仅当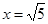 时,“=”成立,∴要使不等式
时,“=”成立,∴要使不等式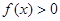 对任意
对任意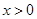 恒成立,只需
恒成立,只需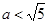 ,即实数
,即实数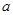 的取值范围是
的取值范围是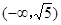 ;
; (2)∵
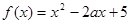 ,∴其图像对称轴为
,∴其图像对称轴为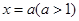 ,根据二次函数的图像,可知
,根据二次函数的图像,可知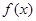 在
在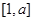 上单调递减,∴当
上单调递减,∴当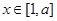 时,其值域为
时,其值域为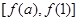 ,又由
,又由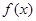 的值域是
的值域是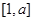 ,
,∴
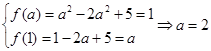 .
.
练习册系列答案
相关题目
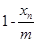 的乘积成正比,比例系数为
的乘积成正比,比例系数为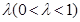 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,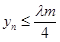 ;
; 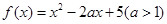 .
.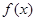 的定义域和值域均是
的定义域和值域均是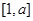 ,求实数
,求实数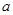 的值;
的值;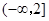 上是减函数,且对任意的
上是减函数,且对任意的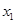 ,
,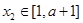 ,总有
,总有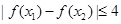 ,求实数
,求实数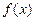 ,
,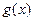 分别由下表给出
分别由下表给出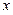
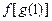 的值为 ;满足
的值为 ;满足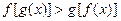 的
的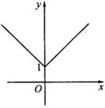
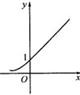
 的值.
的值.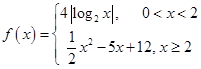 ,若存在实数
,若存在实数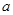 、
、 、
、 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则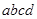 的取值范围是 .
的取值范围是 .