题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{-2},}&{x>0}\\{{2}^{x},}&{x≤0}\end{array}\right.$,则方程f(x)-$\frac{1}{2}$x=1的解的个数为3.分析 作函数f(x)=$\left\{\begin{array}{l}{{x}^{-2},}&{x>0}\\{{2}^{x},}&{x≤0}\end{array}\right.$与直线y=$\frac{1}{2}$x+1的图象,从而求解.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{{x}^{-2},}&{x>0}\\{{2}^{x},}&{x≤0}\end{array}\right.$与直线y=$\frac{1}{2}$x+1的图象如下,
结合图象可得,有3个交点;
故方程有3个解;
故答案为:3.
点评 本题考查了学生的作图与用图的能力,考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
15.已知tanα=3,则cos2α=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
13.正方形ABCD的边长为2,E是线段CD的中点,F是线段BE上的动点,则$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是( )
| A. | [1,0] | B. | $[-1,\frac{4}{5}]$ | C. | $[-\frac{4}{5},1]$ | D. | [0,1] |
10.在等比数列{an}中,a3,a9是方程3x2-11x+9=0的两个根,则a5a6a7=( )
| A. | 3$\sqrt{3}$ | B. | $\frac{11}{2}$ | C. | ±3$\sqrt{3}$ | D. | 以上皆非 |
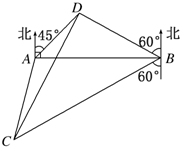 某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.
某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.