题目内容
13.正方形ABCD的边长为2,E是线段CD的中点,F是线段BE上的动点,则$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是( )| A. | [1,0] | B. | $[-1,\frac{4}{5}]$ | C. | $[-\frac{4}{5},1]$ | D. | [0,1] |
分析 建立直角坐标系,求出B、C、E的坐标,求出直线BE的方程,设F(x,$\frac{1}{2}x$),(0≤x≤2),由向量的坐标运算求出$\overrightarrow{BF}$、$\overrightarrow{FC}$的坐标,由向量的数量积坐标运算求出$\overrightarrow{BF}•\overrightarrow{FC}$的表达式,利用二次函数的性质求出$\overrightarrow{BF}•\overrightarrow{FC}$的最值和值域.
解答 解:以AB为y轴,BC为x轴建立直角坐标系,
∵正方形ABCD的边长为2,E是线段CD的中点,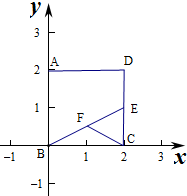
∴B(0,0),C(2,0),E(2,1),
则直线BC的方程是y=$\frac{1}{2}x$,
设F(x,$\frac{1}{2}x$)(0≤x≤2),
则$\overrightarrow{BF}$=(x,$\frac{1}{2}x$),$\overrightarrow{FC}$=(2-x,-$\frac{1}{2}x$),
则$\overrightarrow{BF}•\overrightarrow{FC}$=x(2-x)$-\frac{1}{4}{x}^{2}$=$-\frac{5}{4}{x}^{2}+2x$,(0≤x≤2),
∵函数y=$-\frac{5}{4}{x}^{2}+2x$的对称轴x=$\frac{4}{5}$,
∴当x=$\frac{4}{5}$时,函数y=$-\frac{5}{4}{x}^{2}+2x$取到最大值是$\frac{4}{5}$,
当x=2时,函数y=$-\frac{5}{4}{x}^{2}+2x$取到最小值是-1,
故$\overrightarrow{BF}•\overrightarrow{FC}$的取值范围是[-1,$\frac{4}{5}$],
故选:B
点评 本题考查向量的数量积坐标运算,向量的坐标运算,以及二次函数的性质,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{56}{65}$ | B. | $\frac{33}{65}$ | C. | $-\frac{56}{65}$ | D. | $-\frac{33}{65}$ |
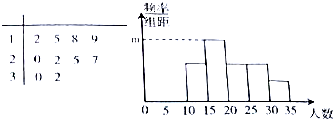 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))