题目内容
15.已知tanα=3,则cos2α=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
分析 由条件利用同角三角函数的基本关系,二倍角的余弦公式求得cos2α的值.
解答 解:∵tanα=3,则cos2α=$\frac{{cos}^{2}α{-sin}^{2}α}{{cos}^{2}α{+sin}^{2}α}$=$\frac{{1-tan}^{2}α}{{1-tan}^{2}α}$=$\frac{1-9}{1+9}$=-$\frac{4}{5}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系,二倍角的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
7.参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,可见部分信息如下,据此计算得到:参加数学抽测的人数n、分数在[90,100]内的人数分别为( )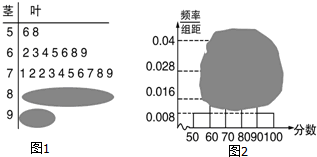

| A. | 25,2 | B. | 25,4 | C. | 24,2 | D. | 24,4 |