题目内容
14.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:(1)若m⊥α,n∥α,则m⊥n;
(2)若α∥β,β∥γ,n⊥α,则n⊥γ;
(3)若m∥α,n∥α,则m∥n;
(4)若α⊥γ,β⊥γ,则α∥β.
其中真命题的序号是(1)(2).
分析 利用空间线面垂直、面面平行、线面平行、面面垂直的性质定理和判定定理分别分析四个命题,得到正确答案.
解答 解:对于(1),若m⊥α,n∥α,根据线面平行、线面垂直的性质定理得到m⊥n;故(1)正确;
对于(2),若α∥β,β∥γ,得到α∥β,又n⊥α,则n⊥γ;故(2)正确;
对于(3),若m∥α,n∥α,则m与n相交,平行或者异面;故(3)错误;
对于(4),若α⊥γ,β⊥γ,则α与β可能垂直,如墙角的三个面的关系.
故答案为:(1)(2)
点评 本题考查了空间线面垂直、面面平行、线面平行、面面垂直的性质定理和判定定理的运用,熟记定理,正确运用是关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
4.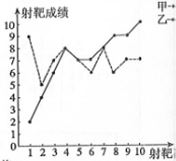 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
(Ⅰ)填写下表:
(Ⅱ)请从四个不同的角度对这次测试进行分析:
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示(Ⅰ)填写下表:
| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
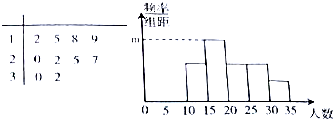 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))