题目内容
16. 某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.
某海域的东西方向上分别有A,B两个观测点(如图),它们相距5(3+$\sqrt{3}$)海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距20$\sqrt{3}$海里的C点有一救援船,其航行速度为30海里/小时.(Ⅰ)求B点到D点的距离BD;
(Ⅱ)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
分析 (Ⅰ)利用正弦定理,求出BD,
(Ⅱ)在△DCB中,利用余弦定理求出CD,根据速度求出时间.
解答 解:(Ⅰ)由题意知AB=5(3+$\sqrt{3}$)海里,
∠DBA=90°-60°=30°,∠DAB=90°-45°=45°,
∴∠ADB=180°-(45°+30)°=105°,…(2分)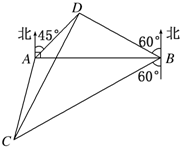
在△DAB中,由正弦定理得$\frac{DB}{sin∠DAB}$=$\frac{AB}{sin∠ADB}$,
∴DB=$\frac{AB•sin∠DAB}{sin∠ADB}$=$\frac{5(3+\sqrt{3})•sin45°}{sin105°}$
=$\frac{5(3+\sqrt{3})•sin45°}{sin45°cos60°+cos45°sin60°}$
=$\frac{5\sqrt{3}(\sqrt{3}+1)}{\frac{\sqrt{3}+1}{2}}$=10$\sqrt{3}$(海里) …(6分)
(Ⅱ)在△DBC中,∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,…(8分)
BC=20$\sqrt{3}$(海里),由余弦定理得
CD2=BD2+BC2-2BD•BC•cos∠DBC=300+1200-2×10$\sqrt{3}$×20$\sqrt{3}$×$\frac{1}{2}$=900,…(10分)
∴CD=30(海里),则需要的时间t=$\frac{30}{30}$=1(小时).…(11分)
答:救援船到达D点需要1小时.…(12分)
点评 本题考查正弦定理以及余弦定理的应用,解三角形的实际问题的应用,考查计算能力.

练习册系列答案
相关题目
7.参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,可见部分信息如下,据此计算得到:参加数学抽测的人数n、分数在[90,100]内的人数分别为( )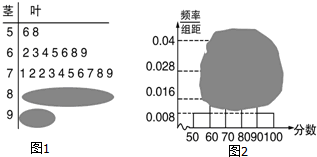

| A. | 25,2 | B. | 25,4 | C. | 24,2 | D. | 24,4 |
11. 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |