题目内容
15.已知在极坐标系中,曲线C1:2ρcosθ=1与曲线C2:ρ=2cosθ,(1)求出曲线C1与曲线C2的直角坐标方程;
(2)求出曲线C1与曲线C2的相交的弦长.
分析 (1)利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\\{{ρ}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$即可得出;
(2)曲线C1与曲线C2的方程联立解出交点坐标即可得出.
解答 解:(1)∵曲线C1:2ρcosθ=1,
∴2x=1 即$x=\frac{1}{2}$.
∵曲线C2:ρ=2cosθ,两边都乘上ρ,可得ρ2=2ρcosθ.
∴x2+y2=2x.
(2)将极坐标方程化为普通方程为$x=\frac{1}{2}$与x2+y2=2x,
联立方程组成方程组求出两交点的坐标$(\frac{1}{2},\frac{{\sqrt{3}}}{2})$和$(\frac{1}{2},-\frac{{\sqrt{3}}}{2})$,
故弦长=$|-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}|$=$\sqrt{3}$.
点评 本题考查了把极坐标方程化为直角坐标方程的方法、圆与圆的相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.阅读如图的程序框图,则输出的S( )
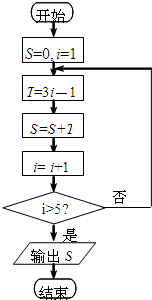

| A. | 6 | B. | 14 | C. | 26 | D. | 40 |
20.已知随机变量X服从正态分布N(1,σ2),且P(X≤0)=0.1,则P(X>2)=( )
| A. | 0.9 | B. | 0.1 | C. | 0.6 | D. | 0.4 |
4.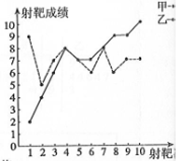 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
(Ⅰ)填写下表:
(Ⅱ)请从四个不同的角度对这次测试进行分析:
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
 甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示
甲、乙两人在相同的条件下各射靶10次,每次射靶成绩均为整数(单位:环),如图所示(Ⅰ)填写下表:
| 平均数 | 方差 | 中位数 | 命中9环及以上 | |
| 甲 | 1.2 | 7 | ||
| 乙 | 3 |
①从平均数与方差相结合的角度分析偏离程度;
②从平均数与中位数相结合的角度分析谁的成绩好些;
③从平均数和命中9环以上的次数看谁的成绩好些;
④从折线图上两人射击命中环数及走势分析谁更有潜力.
5.若a>b,则下列不等式成立的是( )
| A. | algx>blgx(x>0) | B. | ax2>bx2 | C. | a2>b2 | D. | $\frac{a}{{{2^x}+1}}>\frac{b}{{{2^x}+1}}$ |
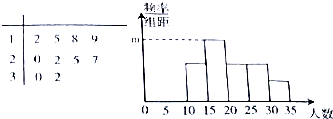 从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))
从某校随机抽取10个班,调查各班中有网购经历的人数,所得数据的茎叶图和频率分布直方图如图所示.(分组区间依次为[10,15),[15,20),[20,25),[25,30),[30,35))