题目内容
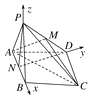
【题目】如图，已知四棱锥P－ABCD，底面ABCD为菱形，且∠DAB＝60°，△PAB是边长为a的正三角形，且平面PAB⊥平面ABCD，已知点M是PD的中点．
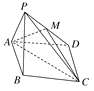
(1)证明：PB∥平面AMC；
(2)求直线BD与平面AMC所成角的正弦值．
【答案】（1）见解析；（2）
【解析】试题分析：（1）连接BD交AC于点O，由三角形中位线可得OM∥PB. 再根据线面平行判定定理得结论（2）先根据空间直角坐标系，再设立各点坐标，根据方程组解得平面法向量，根据向量数量积求向量夹角，最后根据线面角与向量夹角互余关系得结果．
试题解析：(1)证明：连接BD交AC于点O，连接OM，因为四边形ABCD为菱形，OB＝OD，又M为PD的中点，所以OM∥PB.
由PB平面AMC，OM平面AMC，所以PB∥平面ACM.
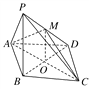
(2)取AB的中点N，连接PN，ND，则∠AND＝90°，
分别以NB，ND，NP为x轴、y轴、z轴建立空间直角坐标系N－xyz，
则B
，C
，
A
，D
，P
，M
，
则
＝
，
＝
.
设平面AMC的法向量为n＝(x，y，z)，
则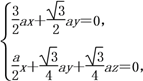
令y＝
，则x＝－1，
z＝－
，即n＝
.又
＝
，设直线BD与n所成的角为θ，则cosθ＝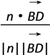
＝
，故直线BD与平面AMC所成角的正弦值为.
练习册系列答案
相关题目
【题目】某零售公司从1月至6月的销售量与利润的统计数据如下：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量 | 6 | 8 | 12 | 13 | 11 | 10 |
利润 | 12 | 16 | 26 | 29 | 25 | 22 |
（1）根据2月至5月4个月的统计数据，求出
关于
的回归直线方程
.（
的结果用分数表示）；
（2）若由回归直线方程得到的估计数据与实际数据的误差均不超过1万元，则认为得到的回归直线方程是有效的.试用1月和6月的数据估计所得的回归直线方程是否有效？
参考公式：
，
.
参考数据：
，
.
