题目内容
5.已知函数y=f(x),x∈[0,+∞),已知当x∈[0,4]时,f(x)=x2-4x,若对[0,+∞)内任意实数x,恒有f(x+4)=m•f(x)(m∈R,m≠0)成立,求函数f(x)的值域.分析 当x∈[0,4]时,f(x)=x2-4x∈[-4,0],结合函数的伸缩变换原则,对m进行分类讨论,可得不同情况下函数f(x)的值域.
解答 解:∵当x∈[0,4]时,f(x)=x2-4x∈[-4,0],
∵对[0,+∞)内任意实数x,恒有f(x+4)=m•f(x),
故当m∈(0,1]时,函数f(x)的值域为[-4,0],
当m∈(1,+∞)时,函数f(x)的值域为(-∞,0],
当m∈(-∞,-1)时,函数f(x)的值域为R;
m∈[-1,0)时,函数f(x)的值域为[-4,-4m]
点评 本题考查的知识点是函数图象的伸缩变换,熟练掌握函数的伸缩变换原则,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.“a=-1”是“过点P(2,1)有且只有一条直线与圆R:x2+y2+2ax+ay+2a2+a-1=0相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
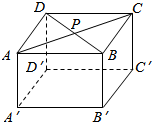 如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )
如图,在长方体ABCD-A′B′C′D′中,P是对角线AC与BD的交点,若P为四棱锥的顶点,棱锥的底面为长方体的一个面,则这样的四棱锥有( )