题目内容
20.已知(2$\sqrt{x}$i+$\frac{1}{{x}^{2}}$)n,i是虚数单位,x>0,n∈N*.(1)如果展开式中的倒数第3项的系数是-180,求n的值;
(2)对(1)中的n,求展开式中系数为正实数的项.
分析 (1)根据二项式的展开式中倒数第3项的系数,列出方程,求出n的值;
(2)由(1)中n的值,利用二项展开式的通项公式,求出展开式中系数为正实数的项.
解答 解:(1)∵(2$\sqrt{x}$i+$\frac{1}{{x}^{2}}$)n,i是虚数单位,x>0,n∈N*.
∴其展开式中的倒数第3项为
${C}_{n}^{n-2}$•${(2\sqrt{x}i)}^{2}$•${(\frac{1}{{x}^{2}})}^{n-2}$=-4${C}_{n}^{2}$•x5-2n;
它的系数是-4${C}_{n}^{2}$=-180,
即${C}_{n}^{2}$=45,
解得n=10;
(2)当n=10时,
Tr+1=${C}_{10}^{r}$•${(2\sqrt{x}i)}^{10-r}$•${(\frac{1}{{x}^{2}})}^{r}$
=${C}_{10}^{r}$•210-r•i10-r•${x}^{5-\frac{5}{2}r}$,
令10-r=0、4、8,
得r=10、6、2;
∴当r=10时,T11=x-20,
r=6时,T7=${C}_{10}^{6}$•26•x-5,
r=2时,T3=${C}_{10}^{2}$•28;
∴展开式中系数为正实数的项为
T11=x-20,T7=${C}_{10}^{6}$•26•x-5,T3=${C}_{10}^{2}$•28.
点评 本题考查了二项式定理的应用问题,也考查了复数的运算问题,是综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若圆x2+y2-4x-4y-10=0上有三个不同的点到直线l:ax+by=0的距离为2$\sqrt{2}$,则直线l斜率k的取值为( )
| A. | 2-$\sqrt{3}$,2+$\sqrt{3}$ | B. | 2-$\sqrt{5}$,2+$\sqrt{5}$ | C. | 2-$\sqrt{3}$,2+$\sqrt{5}$ | D. | 2+$\sqrt{3}$,2+$\sqrt{5}$ |
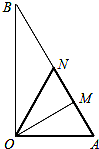 如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中OA=3km,OB=3$\sqrt{3}$km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.