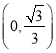题目内容
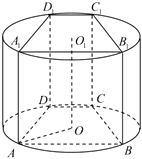
【题目】如图,圆柱体木材的横截面半径为![]() ,从该木材中截取一段圆柱体,再加工制作成直四棱柱
,从该木材中截取一段圆柱体,再加工制作成直四棱柱![]() ,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心
,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心![]() 在梯形
在梯形![]() 内部,
内部,![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
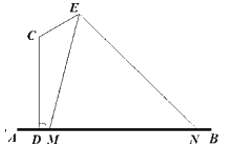
(1)求梯形![]() 的面积;
的面积;
(2)当![]() 取何值时,直四棱柱
取何值时,直四棱柱![]() 的体积最大?并求出最大值(注:木材的长度足够长)
的体积最大?并求出最大值(注:木材的长度足够长)
【答案】(1)![]() ;(2)当
;(2)当![]() 时,体积取最大值为
时,体积取最大值为![]()
【解析】
(1)根据等腰梯形的性质,结合锐角三角函数的定义可以求出![]() 、以及等腰梯形的高、
、以及等腰梯形的高、![]() 、
、![]() 的表达式,最后求出等腰梯形的面积表达式即可;
的表达式,最后求出等腰梯形的面积表达式即可;
(2)利用棱柱的体积公式求出四棱椎体积的表达式,令![]() ,进行换元,利用导数求出体积的最大值即可.
,进行换元,利用导数求出体积的最大值即可.
(1)由条件可得,![]() ,所以梯形的高
,所以梯形的高![]() .
.
又![]() ,
,![]() .所以梯形
.所以梯形![]() 的面积
的面积
![]()
![]()
![]() .
.
(2)设四棱柱![]() 的体积为
的体积为![]() ,因为
,因为![]() ,
,
所以![]() .
.
设![]() ,因为
,因为![]() ,所以
,所以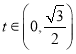 ,所以
,所以![]() ,
,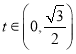 ,
,
由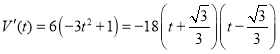 ,令
,令![]() ,得
,得![]() ,
,
![]() 与
与![]() 的变化情况列表如下:
的变化情况列表如下:
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以,![]() 在
在![]() 时取得极大值,即为最大值,且最大值
时取得极大值,即为最大值,且最大值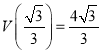 .此时
.此时![]()
答:当![]() 时,四棱柱
时,四棱柱![]() 的体积取最大值为
的体积取最大值为![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目