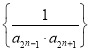题目内容
【题目】有一个长方形木块，三个侧面积分别为8，12，24，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为（ ）
A.2B.
C.4D.
【答案】B
【解析】
先求长方体从同一顶点出发的三条棱的长度，从而可得正四面体模型棱长的最大值.
设长方体从同一顶点出发的三条棱的长分别为
，则
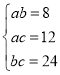，故
，
若能从该长方体削得一个棱长最长的正四面体模型，
则该四面体的顶点必在长方体的面内，
过正四面体的顶点作垂直于长方体的棱的垂面切割长方体，
含正四面体的几何体必为正方体， 故正四面体的棱长为正方体的面对角线的长，
而从长方体切割出一个正方体，使得面对角线的长最大，
需以最小棱长
为切割后的正方体的棱长切割才可，
故所求的正四面体模型棱长的最大值
.
故选：B.
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
