题目内容
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;
;
(2)不存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立,理由见解析.
成立,理由见解析.
【解析】
(1)利用二次不等式解集的性质与韦达定理求解得![]() ,再代入
,再代入![]() 了与基本不等式求最值即可.
了与基本不等式求最值即可.
(2)由题可知若存在则![]() ,根据对数不等式性质可知
,根据对数不等式性质可知![]() ,再分析二次函数的对称轴与区间的位置关系求得
,再分析二次函数的对称轴与区间的位置关系求得![]() 的最值分析即可.
的最值分析即可.
(1)依题意得,2和3是方程![]() 的两根
的两根
由韦达定理可知:![]()
∴![]()
又∵![]() ,∴
,∴![]()
当且仅当![]() 时等号成立,
时等号成立,
所以![]() 的最小值为
的最小值为![]() .
.
(2)假设存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立
成立
∴![]()
∵![]() 时,
时,![]() ,∴
,∴![]()
∴![]() 在
在![]() 成立
成立
记![]() ,其对称轴为
,其对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]()
由![]() ,∴
,∴![]() …
…
②当![]() ,即
,即![]() 时,
时,![]()
由![]() ,∴
,∴![]()
综上所述,不存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立.
成立.

 阅读快车系列答案
阅读快车系列答案【题目】某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,若
,每单提成4元,若![]() ,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若
,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
表1:美团外卖配送员甲送餐量统计
日送餐量x(单) | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2:饿了么外卖配送员乙送餐量统计
日送餐量x(单) | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)设美团外卖配送员月工资为![]() ,饿了么外卖配送员月工资为
,饿了么外卖配送员月工资为![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小关系
的大小关系
(2)将4月份的日送餐量的频率视为日送餐量的概率
(ⅰ)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y)
(ⅱ)请利用所学的统计学知识为小王作出选择,并说明理由.
【题目】某中学为调查高三学生英语听力水平的情况,随机抽取了高三年级的80名学生进行测试,根据测试结果绘制了英语听力成绩(满分为30分)的频率分布直方图,将成绩不低于27分的定为优秀
(1)根据已知条件完成下面的![]() 列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
列联表,并据此资料判断是否有90%的把握认为英语听力成绩是否优秀与性别有关?
英语听力优秀 | 非英语听力优秀 | 合计 | |
男同学 | 10 | ||
女同学 | 36 | ||
合计 |
(2)将上述调查所得到的频率视为概率,现在从该校高三学生中,采取随机抽样方法每次抽取1名学生,共抽取3次,记被抽取的3名学生中“英语听力优秀”的人数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望E(X)
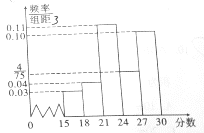
参考公式: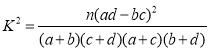 ,其中
,其中![]()
参考临界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |