题目内容
【题目】已知![]() =
=![]() 是矩阵M=
是矩阵M=![]() 属于特征值λ1=2的一个特征向量.
属于特征值λ1=2的一个特征向量.
(Ⅰ)求矩阵M;
(Ⅱ)若![]() ,求M10a.
,求M10a.
【答案】(Ⅰ)M=![]() ;(Ⅱ)M10
;(Ⅱ)M10![]() =
=![]() .
.
【解析】
试题(Ⅰ)依题意,M![]() =
=![]() ,从而
,从而![]() ,由此能求出矩阵M.
,由此能求出矩阵M.
(Ⅱ)(方法一)由(Ⅰ)知矩阵M的特征多项式为f(λ)=(λ﹣1)(λ﹣2),矩阵M的另一个特征值为λ2=1,设![]() =
=![]() 是矩阵M属于特征值λ2=1的特征向量,由已知得
是矩阵M属于特征值λ2=1的特征向量,由已知得![]() =
=![]() ,由此能求出M10
,由此能求出M10![]() .
.
(Ⅱ)(方法二)M2=MM=![]() ,
,![]() ,M5=M3M2,M10=M5M5,由此能求出M10
,M5=M3M2,M10=M5M5,由此能求出M10![]() .
.
解:(Ⅰ)依题意,M![]() =
=![]() ,
,
![]() ,
,
∴![]() ,
,
解得a=1,b=2.
∴矩阵M=![]() .
.
(Ⅱ)(方法一)由(Ⅰ)知矩阵M的特征多项式为f(λ)=(λ﹣1)(λ﹣2),
∴矩阵M的另一个特征值为λ2=1,
设![]() =
=![]() 是矩阵M属于特征值λ2=1的特征向量,
是矩阵M属于特征值λ2=1的特征向量,
则![]() ,
,
∴![]() ,取x=1,得
,取x=1,得![]() =
=![]() ,
,
∴![]() ,
,
∴M10![]() =
=![]() =
=![]() .
.
(Ⅱ)(方法二)M2=MM=![]() ,
,
![]() ,
,
M5=M3M2=![]() =
=![]() ,
,
M10=M5M5=![]() =
=![]() ,
,
∴M10![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】在衡阳市“创全国文明城市”(简称“创文”)活动中,市教育局对本市A,B,C,D四所高中学校按各校人数分层抽样,随机抽查了200人,将调查情况进行整理后制成下表:
学校 | A | B | C | D |
抽查人数 | 10 | 15 | 100 | 75 |
“创文”活动中参与的人数 | 9 | 10 | 80 | 49 |
假设每名高中学生是否参与“创文”活动是相互独立的
(1)若本市共8000名高中学生,估计C学校参与“创文”活动的人数;
(2)在上表中从A,B两校没有参与“创文”活动的同学中随机抽取2人,求恰好A,B两校各有1人没有参与“创文”活动的概率;
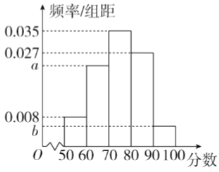
(3)在随机抽查的200名高中学生中,进行文明素养综合素质测评(满分为100分),得到如上的频率分布直方图,其中![]() .求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).
.求a,b的值,并估计参与测评的学生得分的中位数.(计算结果保留两位小数).