题目内容
【题目】已知函数f(x)=aex﹣2x+1.
(1)当a=1时,求函数f(x)的极值;
(2)若f(x)>0对x∈R成立,求实数a的取值范围
【答案】(1)极小值为3﹣2ln2,无极大值;(2)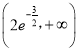 .
.
【解析】
(1)求导,判断函数单调性,根据单调性求得极值;
(2)分离参数,构造函数,求解函数的最值,即可求得参数的范围.
(1)当a=1时,f(x)=ex﹣2x+1,则f′(x)=ex﹣2,
令f′(x)<0,解得x<ln2;令f′(x)>0,解得x>ln2;
故函数f(x)在(﹣∞,ln2)上递减,在(ln2,+∞)上递增,
故函数f(x)的极小值为f(ln2)=2﹣2ln2+1=3﹣2ln2,无极大值;
(2)f(x)>0对x∈R成立,即为![]() 对任意x∈R都成立,
对任意x∈R都成立,
设![]() ,则a>g(x)max
,则a>g(x)max
![]() ,
,
令g′(x)>0,解得![]() ;令g′(x)<0,解得
;令g′(x)<0,解得![]() ;
;
故函数g(x)在![]() 递增,在
递增,在![]() 递减,
递减,
∴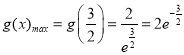 ,
,
故实数a的取值范围为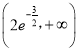 .
.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目